Формула (18.191) для согласно рис. 18.37, г принимает вид

4с Y . - , 4с

I sin3v/ai; = ---cos3i;,.

ка

откуда с учетом соотношений (18.195) находим

.2 Au2

з =---Ча-Ь пща>Ь.

(18.197)

В частности, для идеальной релейной характеристики из формул (18.196) и (18197), полагая= О, получим:

= 0, гз =

(18.197)

Рассмотрим два при.мера, иллюстрирующих процесс отыскания высших гар.моник при автоколебаниях, а также уточнения первой гармоники за счет учета низших.

П р и . е р 1. Исследуем следящую систему с нелинейностью типа насыщения, автоколебания в которой в перво.м приближении х = а sin со/уже были найдены ранее, в при.мере 1 § 18.3, в общем виде.

Пусть теперь заданы параметры системы: Г = 0,005 с. Го = 0,4 с, А = 140 с, к = Ш с, kf, = 0,5 с.

Они удовлетворяют соотношению (18.76). Следовательно, здесь имеет место случай, изображенный иа рис.18.14, б, причем согласно (18.79) и (18.74) = 166 6-, =125 с. Заданное значение k лежит между ними, что соответствует области наличия двух периодичес-кихрежимов. Выведенные выше формулы первого приближения (18.70) и (18.71) при этом дают для неустойчивого режима а = 2,29 S, 0) = 118,2 с , а для устойчивого режима а = 21,4 й, 03 = 44,8 с \ причем а = 7,08 В (в точке оз рис. 18.14, б).

Иаиболыпий интерес представляет первое(неустойчивое) периодическое решение. Оно указывает границу для начальных условий, вне которой переходный процесс в системе будет расходиться, стрсмясь к автоко-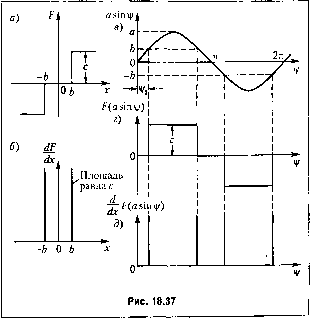

лебииям с очень болыной амнлигулой а 21,4 в, что практически можно считать неустойчивостью системы в больнюм. Поэтому уточнение решения с вычислением выс-uHix гармоник произведем только для первого периодического решения.

Для данной нелинейности (рис. 18.13, а) но фор.мула.м (18.191) находим выражения:

(18.199)

Из формул (18.192) и (18.68) получаем относительную амплитуду 83 и фазу фз третьей гармоники в виде

(-9еда))Ч9(?ю2

(97fa)-hl)(972or-hl)

Фз = + arctg-arctg371co- arctg3T2a).

k-9TAo-y

Вычисление по .этим формулам дает

63 =0,0317, Фз- -1,875.

Для уточнения первой гармоники за счет только что вычисленной третьей гармоники находим согласно (18.190) добавки к коэффиниеитам гар.монической линеаризации:

А = Аз6зСозфз, Аг/ = 3гз5з5!пфз,

подставляя которые в (18.188) согласно (18.68) придем к уточненному характеристическому уравнению

(т р+\хт,р+\)p+[k+{т,р+\)kp

л V

м+-Р

+ [k + {Tp + \)kp]q{a) = 0, (18.200)

где апатогично (18.66) и.меем

q = к, при я, < Ь,

2к, <? = -

Ь hi ft-arcsin - + -, 1 -7 а, я, V а

(18.201)

Подставив в уравиепие (18.200) р =ja) и выделив вещественную и мнимую части, нолучим два уравнения:

кд{щ) + Щ-\Т +7 +7 g,7(a,)]co? f7;A=0;

V to )

( л л

1 + \q{a )]а), + kAq + k- м, - ТоТо)? - Т-, = 0.

\ т ) со

Эти уточненные уравнения отличаются от прежних уравнений первого приближения несколькими добавочными членами, но способ решения их остается прежним. И:) последнего уравне1И1я находим

СОГ =-

\ + kq{a{) + kM + k

(18.202)

а из первого

/ л Л

q{aO + Aq

(18.203)

Задаваясь разными значениями амплитуды а, и вычисляя каждый раз по формулам (18.201)-(18.203) значения q (а,), fsi\ и , нолучим графики а, (it) тина рис. 18.14, но уже для уточненного значения а.\И1литуды а первой гармоники периодического решения.

Для заданного 31шчения k = 140 это уточнение дает а, = 2,39 В, м, = 117,8 с . Значения эти достаточно близки к величинам перво10 приближения, а подсчитанная выше амплитул.а третьей гармоники достаточно мала.

Пример 2. Пусть в системе авто.матического управления используется двухфазный двигатель, описываемый пстинейны.м уравнешге.м (18.119). В примере 7 § 18.3 найдены автоколебания для первого приближения в общем виде. Рассмотрим с;ледую-щий числовой пример;

Гз = 0,5с, 7, =0,1 с, , = 26,5 с

с двумя варианта.ми пелипейиости:

а) слабая нелинейность

ft, =0,01, Й2 = 0,1, йз = 0,002;

б) сильная нелинейность

ft, =0,1, ft2=l, йз = 0,166.