78 Непрерывные линейные системы автоматического управления

При исиользоваиии оиерациоииого усилителя (рис. 4.19, а) изодромное звено может быть получено посредством примепения RC-пспи в обратной связи.

В системах управления часто находят применение изодромные звенья, построенные на базе интегрирующего привода (рис. 4.19, в). В это.м случае входное напряжение Mj поступает непосредственно на выход. Кроме того, это же напряжение поступает на вход интегрирующего привода. Угол поворота валика последнего, в соответствии с изложенным выше, пропорциона-тен интегралу от входного напряжения На выходном валике устанавливается какой-либо датчик (Д) представляющий собой линейный преобразователь угла поворота в напряжение, например нотенцио-метр или линейный врапщющийся трансформатор. Напряжение этого преобразователя 3 су.ммнруется с напряжением w,. Эта сумма и представляет собой выходное напряжение

Таки.м образом, для схемы, изображешюй на рис. 4.19, в,

.(P) = f.(p).

Тр) Тр

где Т- коэффициент пропорциональности между скоростью изменения выходного напряжения датчика интегрирующего привода и напряжением на его входе. Коэффициент передачи идеального интегрирующего звена в этом случае равен k = \/Т.

Временные характеристики звена представлены в табл. 4.4, а частотные - в табл. 4.5.

Л. а. x. строится по выражению

i(co) = 20lg:/ll5l.

Асимптотическая л. а. х. представляет собой две прямые: с отрицателы1ы.м наклоном -20 дБ/дек (при со < 1/Т) и параллельную оси частот (при со > 1/7 )-

Из рассмотрения л. а. х. и л. ф. х. видно, что в области малых частот (меньших, чем сопрягающая частота) звено ведет себя как идеальное интегрирующее и те.м точнее, чем меньше частота.

В области больших частот (больших, чем сопрягающая частота) звено ведет себя как безынерционное с коэффициентом передачи

Свойство звена вводить интегрирующее действие в области малых частот используется для улучшения качественных показателей систе.м автоматического регулирования (см. главу 9).

§ 4.7. Дифференцирующие звенья

1. Идеальное дифференцирующее звено. Звено описывается уравнением

Х2 = k dxj/dt. (4.49)

Передаточная функция звена

W<j}) = kp . (4.50)

Примеры идеальных диф(11еренцируюншх звеньев изображены на рис. 4.20. Единственным идеальным диффереицируюн[и.м звено.м, которое точно описывается уравнением (4.49), является тахогенератор постоянного тока (рис. 4.49, а), если в качестве входной величины рассматривать угол поворота его ротора а, а в качестве выходной - э. д. с. якоря е. В тахогенера-торе постояпиото тока при неиз.меппом потоке возбуждения э. д. с. в якоре пропорциональна скорости вращения: е = kO.. Скорость врап1ения есть производная ио времени от угла поворота: Q = da/dt. Следовательно, е = k da/dt. В режиме, близком к холостому ходу (сопротивление нагрузки велико), можно считать, что напряжение якоря равно э. д. с: и = е. Тогда и = k da/dt.

Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель в режиме дпфферсрщировапия (рис. 4.20, б).

Временные характеристики приведены в табл. 4.6, а частотные - в табл. 4.7.

2. Дифференцирующее звено с замедлением. Звено описывается уравнением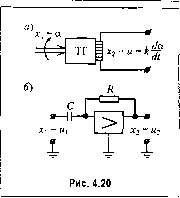

(4.51)

Таблица 4.6. Временные характеристики дифференцирующих звеньев

Тип звеиа и его передаточная функции

Переходная функция

Функция веса

Идеальное дифференцирующее

W(p) = kp

(0(0 = %) =

Дифференцирующее с замедлением

l+Tp

hit)

й(0=е>-1(0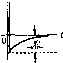

Тип звена и его частотная передаточная функция

Амплит>дио-фазовая

Амплитудная и фазовая

Логарифмические

Идеальное дифференцирующее W(j(u) = kja

i(<0)

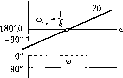Диффсрсицирующее с замедлением

kj(0

\ + j(mT

90° 0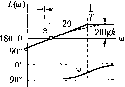