На осповапии (21.47) по первой из ([юр.мул (21.28) паходи.м

f** =- \Г{х -i-Bsin\i;, BcOgcos\j;)(!/\j;, 2я j

что и дает искомую сглаженную характеристик}. При это.м можно воспользоваться для всех типовых нелинейностей готовыми формулами из главы 19 и их графика.ми типа рис. 21.6, а, .заменив везде а и па величину В. Как видим, здесь совершенно отпадает описан[К)е в § 21.2 особое определение функции смещения Ф (х ).

В результате сглаженная характеристика (х°) будет и.меть крутизну .зависяН1ую в обп1ем случае от амплитуды В и частоты (0 внешних вибраций. Если же и.меется нелинейность менее общего вида, а и.менно F{x), то частота о) пе войдет в выражение для f °, как, например, в случае рис. 21.6, а. Однако все же и в этом случае нужно потребовать, чтобы частота содержатась в определенных пределах, позволяюпщх считать воздействие/, (t) по сравпению с/2 (г) медленно меняющимся.

Онре/че..тив таким образо.м сглаженную .характеристику /- (х ), .можно зате.м но уравнению типа (21.31) или (21.44) с использованием линеаризации (21.45) исследовать любые медленно протекаюпше процессы в системе в цело.м обычны.ми методами теории управления. Заметим, что линеаризация по ([формуле (21.45) в дайной задаче справедлива для любых форм нелинейностей, так как .здесь частная производная но-т** совпадаете полной производной.

Что касается уравнения для колебательных составляющих (21.32) и.ш, что то же самое, (21.33), то его нужно нспо.чьзовать в ланпоп задаче только для определения желательной величины частоты о) внешнего периодического воздействия/2 (0. обсс-печиваюП1ей возможность получения решения (21.47) для вынужденных колебаний и вынолпение сделатюго выше предположения о малости вынужденных вибраций на выходе системы Х3. С этой целью подставим равенства (21.47) и (21.48) в уравнеиие (2133). То1-да для удовлетворения последнего уравнения необхо/щ.мо потребовать, чтобы модуль отношения

Q(M,)

был Очень.мал. Следовательно, частота внепшего периодического во.здействия должна лежать за пределами полосы пропускания всей лиией]юй части рассматривае.мого участка системы (блоки 1 и 2).

Кроме того, чтобы амплитуда вынужденных вибраций на выходе систе.мы х3 была ничтожна, нужно взять частоту a) также и за пределами полосы пропускания отдельного блока 2 исследуе.мой системы (рис. 21.10).

Задача 2 . Пусть на какую-нибудь систему автоматического управления (рис. 21.11) воздействует впепшяя вибрационная помеха

/2(0= В sin О)/

-Н8ь

Линейное звено

Линейное звено

Пс.п иней-нос :)всио

F{x.px)

Пинейное увено

Обратная связь

1/2(0

Упраьляе.мьгй объект

И, кроме того, внешнее задающее или возмущающее воздействие(t), которое но отношению к помехе является медленно мепяклпимся. Уравнстше динамики системы приводится к виду (21.24).

Peinenne уравнения (21.24) иптся в виде (21.26), гдех° - полезный сиг-пал управления, а х* - вибрационная по.меха на входе пелинейного звена. Ра;!бив уравнение (21.24) па два, а имеп-1ю на (21.31) и (21.33), необходимо, согласно развитому выше общему методу, определить сначача с помощью (21.33) и (21.29) функцию смещения = Ф (х), после чего можно решать дифференциальное уравие-ime (21,31) относительно переменной х (t) нри заданной функпии /2 (С). Однако в данной .задаче этот обищй .метод 1)ешепия можно упростить. Рассмотри.м два случая.

В том случае, когда вся приведе(И1ая линейная часть системы (рис. 21.11), определяемая передаточной функцией

Рис. 21,11

QiP)

(21.49)

практически не пропускает вибраций с заданной частотой о) , уравнение (21,33) мож-1Ю.записать в виде

52(./а) )

а(./Ч)

Тогда амплитуда вибраций на входе нелипейногозвена будет опреде;1яться формулой

/2.- (21.50)

2 2(Ч,) + У2(Ч)д2

Х(ш ) + Гу2(а) )

где через Х2 (а) ), Уг (oj и Xq (а) ), Tq (o) обозначены вещественные и мнимые части соответственно для выражений 52Ою ) и QOMb)-

Формула (21,50) дает лгнюйпую зависимость а (В) с разными коэффициеита.ми пронорционать-ности для разных частот вибраций а) (рис, 21.12). В частности, для схемы рис. 21.11 oini будут онреде-.тяться структурой линейных б;юков 1 2.

По сравнешно с общей теорией здесь существенно то, что а.мплитуда вибраций а на входе нелинейного звена в это.м случае не зависит от величины В полезного сигпатах*. Поэтому здесь, как

и в задаче 1, отпадает необходимость отыскания функции смещения Ф (.г ) и характеристика нелине11Ного звена по полезному сигналу f ° будет оп редел ятьс-.я непосредственно первой формулой (21.29), представленной гра(})ически, например, иарис. 21.6, . Однако здесь нужно подставить в выражепис f ° или взять па графике [)нс. 21.6, а значение д , определяемое по фор.муле (21.50) или графико.м рис. 21.12. Поэтому, в отличие от задачи 1, здесь даже для простейших нелинейностей очертание характеристики нелинейного звеиа по полезному сигналу (х**) и ее крутизна

,v =0

Рис. 21.13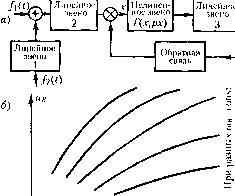

будут зависеть не только от амплитуды В, но и от частоты о) вибрационных помех, а также, конечно, и от параметров линейных блоков / и 2 (i)hc. 21.11), входящих в фор.мулу (21..50).

Рассмотрим далее другой случай, когда первая гармоника вибраций с заданной частотой (Од пропускается линейной частью систе.мы с передаточной функцией (21.49), но все жс ие пропускается каким-либо одни.м б.аоком систе.\1ы. Пусть, нанри.мс!), в схеме па рис. 21.11 вибрации не пропускаются вовсе только управляемым обтектом, а но внутренней обратной связи первая гармоника вибраций с частогой а) проходит. Тогда, вообще говоря, уже нельзя не считаться с зависимостью (21.34) амплитуды вибраций а переменной хот величины полезного сигнала .г . Однако и в этом случае возможно упрощение решения задачи по сравнению с обпдчт теорией, состоящее в том, что при оцрсделеиии функции смещения выбрасывается часть системы, не пропускающая вибраций (рис. 21.13, а).

В это.м случае нужно записать уравнение динамики только остав1Пе11ся части системы (рис. 21.13, а):

Q (p)x -г R(j,)F (X, рх) = 5 (p)J\ (t) + 52, (р)Л (0-

(21.51)

которое будет, конечно, проще общего уравнения (zl.24). Отсюда поаналогии с (21.35) получим уравнение для определения амп.читуды виб[)аций на входе иелннейпого .звена в виде

Х,(ш ) + Т2<.(а) )

X,(a ,co ,x ) + yfl ,a) ,.r )