При помощи подстановки

х(0 = (Ое (13.20)

это уравнение приводится к виду

/2 AP(Odt

±1 + F(t)u = me =Mt). (13.21)

Здесь введено обозначение

f(o.a(o-i-. (.3.22)

При действии единичного и.мпульса f (t) = b(t- d) для урав1гения (13.21) получится решение м = z (t - &, d), которое связано с весовой функцией w (t - d) исходного уравнения (13.19) ira основании фор.мулы (13.20) соотношс1Гием

w{t-x\-&) = z{t-&,&)€ О . (13.23)

Если же положить/, (t) = 8(t- d), то для уравнения (13.21) будет получена весовая функция r(t- д), которая на основании (13.9) связана с решением z {t- ) зависи.мостью

z{t--d,b) = jr(t-u,u)e о &{u-b)du.

Эта зависимость иа основании свойства дельта-функции может быть представлена в виде

z(t--d,\i) = r{t-&,&)€ о В результате из (13.23) и (13.24) получаем

й (13.24)

A-jp(t)dt

(t--d,f>) = r(t-xX)e (13.25)

Дифференциальное уравнение второго порядка. Рассмотрим случай, когда дифференциальное уравнение (13.1) сводится к уравнению второго порядка

cof+а(Ох=/(о. (13,19)

Таким образом, для отыскания <1)ункнии веса да (t - д, -&) необходимо предварительно решить уравнение (13.21), которое приобретает вид

+F(t)u = S(t~&) (13.26)

с пулевы.ми начальными условиями: м (г) = О и M(f) = 0 при t = -в. Полученную при решении весовую функцию и = г (t - -д, Ь) необходимо зате.м подставить в (13.25) и найти Ь (t - Ь, д).

Решение уравнения (13.26) может быть произведено при помощи функций Бес-селя [86]. Для этого функция F(t) должна быть анпроксимировапа отрезками прямых линий, уравнение которых сводится к виду а,- + bjt. Однако это решение является сравнительно сложным.

Ограничимся рассмотрением гак называемого аппроксимирующего репюния, которое .может применяться, если функция f(t) мало изменяется относительно своего среднего большого значения F (рис. 13.4). Это ре(пенне называется аппроксимацией Бриллуина-Вентцеля-Крамера [86].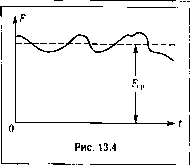

Рассмотрим однородное дифференциальное уравнение

+F(t)u = 0.

(13.27)

Предположим теперь, что для некоторого однородного дифференциального уравнения второго порядка получено частное решение

1 .-iSU)

(13.28)

u,(t) =

5(0= \N(t)dt.

(13.29)

Найдем дифференциальное уравнение, которо.му удовлетворяет решение (13.28). Продифферешшровав его дважды и исключив промежуточные переменные, получаем

d\ dt

1 N 2N

м, =0.

(13.30)

Сравнивая (13.30) и (13.27), видим, что выражение (13.28) будет частным решением уравнения (13.27), если выполняется тождество

F(t)N- 4

<г\ е 1.

Тогда решение (13.21) можно представить в виде

N = N + N,+N2 +... 413.32)

Подставляя этот ряд в (13.31), получаем формулы для определения членов ряда:

1 Ло

2 Лп

1 -V,

2 N,

(13.33)

Часто .можно ограничиться только первым члено.м ряда (13.22), что будет справедливым, если функция F (I) изменяется .медленно, оставаясь в среднем больнюй (рис. 13.4). Тогда

A40 = VW

(13.34)

При выполнении условия F(t)> О в качестве второго частного репюпия можно взять комплексно-сопряженную величину (13.29)

2(0 =

JSU)

Тогда можно нока.зать, что реичение уравнения (13.26) будет щ()йАд)-щ(д)щ(Ь) 2j

или, после подстановки (13.28) и (13.35),

-(t)F(d)

.sin

(13.35)

(1,3,36)

(13.37)

Решепие уравнения (13.31) и отыскание функции Л(;) является сложной задачей вследствие натичия нелинейностей в (13.31). Однако .может быть найдено нри-ближсннос решение (13.31) в виде ряда, если удовлетворяются неравенства