Рис, 6.8

l\V=lmW(jm) ш = а) U=Yi.cW(jw)

co = 0

Рис, 6.9

причем степень числителя не может быть выше степени знаменателя, тп. При подстановке/) = jti) получается частотная передаточная функция разомкнутой системы

6X;w)

(6.20)

Частотная передаточная функция разомкнутой системы представляет собой комплексное число. Иа основании рассмотренных в главе 4 частотных характеристик схнясл ее можно объяснить следуюпщм образом (рис, 6.8). Представим себе систему уп1)авления в разомкнутом состоянии в виде некоторого звена с передаточной фуггк-цией W{p). Если на вход зтого звена подавать сигнал ohhi6kh в виде гармонических колебаний х = Х , sin ш/. с а.мплитудой Х ,., и частотой ш, то в установившемся режиме иа выходе управляемая величина будет изменяться также но гармоническому закону г/ = К , sin (wf + v/) с а.мплитудой Умх- й же частотой и фазовым сдвиго.м vj/. Модуль частотной передаточной функ1и1и представляет собой опгошетгие а.мплитуд выходной и входной величин:

Л(ш) =

(6.21)

а аргумент - сдвиг фаз \/. При постоянном значештн Х , амплитуда У , зависит от частоты входного сигнала: У, = У,(л)- От частоты зависит и сдвиг фаз, или фаза: V = V(w).

Если из.менять частоту входного воздействия от О до и откладывать иа ко.мп-лекспой плоскости точки, соответствующие получающимся комнлексны.м числам, то гео.мет[жческое место этих точек обра,зует амплитудно-фазовую характеристику разомкнутой системы (рис. 6.9).

На амилитудпо-фазовой характеристике для удобства могут отмечаться точки, соответствующие оиределепны.м частота.м, например ш щ, Ш3 и т. д. Вдоль кривой иногда рисуют стрелки, которые показывают направление возрастания частоты ш (рис. 6.9).

В реальных системах всегда удовлетворяется условие т <п. Поэтому при частоте, стремящейся к бесконечности, модуль частотной передаточной функции стремится к пулю и точка с частотой ш-> оо попадает в начало координат.

Для построения а. ф. х. в выражеггии (6.20)можпо выделить вещественную f/(cjo) и .мнимую V{w) части. Однако, если порядок системы > 2, удобнее использовать

Таблица 6.1

Сомножитель

Л( )

v(co)

Tp + i

Vi+7-v

arctg ш 7

Tp-l

Vl+7-V

7t - arctg to Г

-arctg CO 7

!i-rV!

0, co<-;

Л, co> - 7

Г V + 2lTp + 1

arctg

2ЫТ 1

20)7-

t-arctg

., , (o-rV-l T

полярные координаты, определяя модуль Л(ц)) и фазу \/((jo). С этой целью передаточную функни (6.19) целесообразно представить в так называемой стандартной ([юрме:

В(р) 7C(Tiр + i)(x2p + mxlp + 2дзт.)р +1)...

W(p) =

С(Р) р\Т,р + \)(1\р +22Т2Р + Шр-)-

(6.22)

Коэффициент К шзывжтся коэффициентом передачи разомкнутой системы, а постоянные Т( и Г, - постоянными времени. Ко.эффипиепты , могут принимать любые значения от О до 1,

Соответствующая (6.22) частотная передаточная функция разомкнутой системы и.меет вид;

Kjl + jm, )(1 + jcoT)[ (1 - xjw) + 2 ;зТзС0]...

(jay (1 + ;юГ,)[ (1 - Та,)+2 Д ..Тг ] (-1 + М,)...

(6.23)

При таком представлении модуль Л(ц)) = iW(/ )i равен отно 1е1ПГЮ модулей числителя и знаменателя, а ар1умепт (фаза) vI((jo) - разности их apryMcirroB. В свою очередь, модуль произведения комплексных чисел [)авен произведению .модулей, а аргумент - сумме аргументов. Модули и аргументы, соответствующие сомножителям передаточной функции (6.22), приведены в табл. 6.1.

Сформул нруем требования к а. ф. х. разомкнутой системы, при выполнении которых замкнутая система будет устойчивой.

Ограничи.м вначале задачу и будем рас-CMaTpiujaTb только устойчивые в разомкнутом состоянии

системы. Это значит, что в характеристическо.м полиноме разомкнутой сисгемы C(j}), представляюгцсм собой знаменатель передаточной функции (6.22), пет нулевых корней (г = 0), а остальные корни имеют отрицательные BciuecTBeinibie части. Для этого, как ткжазаио в § 6.2, необходн.мо и достаточно, чтобы все коэффициенты полиномов первого и второго порядков были положительными, т. е. в полипо.м С(р) должны входить только сомножители типа Г,/: -t- 1 и Т +2iTjP + i при ,-50. Нижебудет показано, что при определенных условиях первое 01раиичеиие .может быть снято. Введем в рассмотрение вспомогательную функцию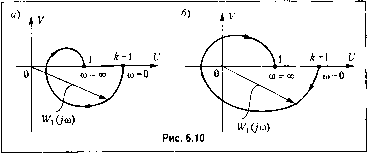

С(р) С(р)

где D(p) - характеристпческиГ! полином замк1гутой системы. Сделаем подстановку р =;со и найдем ко.мплекс

(6.24)

1У,(;а)) =

С(;а))

(6.25)

Будем изменять частоту (о от О до о° и изобразим получившуюся амплитудно-фазовую характеристику VK](/(o) на комплексной плоскости (рис. 6.10). При (0 = 0 при указанных выше условиях согласно (6.23) \V{j(Si) = К, W,(/w) = 1+/С, а при (о = о°, так как m < и, 1У(;(о) = О, Wj(;c)) =1, Определим результнрую1ций угол поворота вектора W,(;(o) при изменении частоты от О до о°. Этот угол представляет собой из.менепие аргумента (6.25), который равен разности аргументов числтеля и зпа.мепателя i/2.

Если замК1гутая система устойчива, то в полином В{р) входят только сомножители первого и второго порядка с положительпы.ми коэффициентами, аналогичные указанным выше сомножителям полинома С(/?). Аргумент первого из них, как еле-

дует из табл. 6.1, изменяется от О до -, а второго - от О до п. Таким образом, при изменении частоты от О до °о аргумент D(;(o) изменяется па величину Vj/, = и-, где п - степень полинома /.)(/?). Степень полинома С(р) такая же, как и полиш)ма Т){р). Поэтому аргумент C{jti>) изменяется на такую же величину; i - Результирующий угол поворота Wijiei) равен нулю: 1/ = - v/2 0. Это означает, что для устойчивой за.мкнутой систе.мы годограф вектора Wi(;a)) не должен охватывать начало координат (рис. 6.10, а).