будет задана величина 6 в начальной точке первого участка процесса, то все вьнпена-ппсапное решение для пе1)еходного процесса в системе станет определенным. Такой метод решения задачи улзыплслсяметодам припасовытиия.

Выясним теперь, возможны ли в данной системе автоколебания, т. е, устойчивое пе])Иодическс)е pcnieime. Для этого нужно, очевидно, чтобы в конце D одного периода

колебаний (рнс. 16.4, 6) получились точно такие же значения 0 и О, какие были в начале его А. Легко заметить, что при этом оба полупериода {АВ н BD) должны быть одинаковыми вследствие си.м.метрии характе1)истики (рнс. 16.4, а). Поэто.му для оп-])еде,тепия автоколебаний достаточно рассмотреть только один участок АВ и потребовать, чтобы

(16.18)

Обозначив период искомых автоколебаний через 2Т. а дли ге.чьпость участка ЛВ, через 7 , из (16.14) найдем

Подставляя сюда(16.18)и.замечая,что нз(16.1б) Э =С, -kc, получаем выраже-

С,(1-ье ) = 2/t,c.

(16.19)

в котором содержатся две неизвестные: С, и Г. Величину (длительность участка/17i) можно вы()азнть из (1 б, 15), так как известно, что в конце участка Э = -Ь. Из (16.15) и (16.16) при это.м находп.м

Т,С,(1-е )-/,?,с7 = -2/;.

Подставив сюда значение С, из (16.19), получим уравнение для определения полупериода автоколебаний:

7 Т b

271 271 kcT,

(16.20)

Это траисцепдептпое уравпение для Глегко решается фафнческн (i)hc. 16.6) пересечением двух кривых:

. Т Т h

Если найдено вешественпое положительное значение для 7, то это свидетельствует о наличии перноД ческого решения в данной систе.ме. Чтобы доказать, что

-- = Ф,(х .г ...,.г ,у,я), j

= Ф.2(Х,Х2.....X, f,g),

5- = Ф (.Г .Г2,...,Х ,/,й)

(16.21)

с начал ьпы.ми условия.ми

-г, =.г-,о, .г-2-Х2о, ..., -r = .v o при t =0,

где:г Х2, х - переменные, являюпшеся иско.мыми функциями времени, приче.м .г, может обозначать управляемую величину, а.Г2,.. .,х - вспомогательные переменные; f ig- возмущающее и задающее во.здействия.

Пусть, например, в уравнениях (16.21) будет п 3 (систе.ма третьего порядка). Переменные х 2, Х3 здесь .могут иметь любой физический смысл. Но условно их можно представить как прямоугольные координаты некоторой точки М(рис. 16.7, а).

В peajibHOM процессе управления в каждый .мо.мент времени величины х Х2, х- имеют bhojTik; опреде.тенныс значения. Это соответствует вподше оп[)еделет10му по;ю-Жешпо точки М в пространстве (рис, 16,7, й). С течением времени в реально.м процессе Величины.г .Г2,ХзОпределенны.м образом изменяются. Это соответствует перемещению точки Мв пространстве по определенной траектории. Следовательно, т)аектория Движения точки М.можст служить наглядной геометрической иллюстрацией поведения системы в процессе управления.

Точка Мпа:п>1вается изобретающей точкой, ее траектория наз1>1вается фазовой траекторией, а прост])анство (.г я-2, лз) пазы вается фазовым прострапапвом.

Так как производные по времени от координат точки представляют проекции ее скорости Г) на оси координат, то;н1фферепциалын:.1еуравнения системы в форме (16.21) Представляют собой выражения для проекций скорости v изображающей точки М (рис, 16.7, й) п-л оси координат. Следовательно, по значениям правых частей уравне-Н1й (16.21) в каждый мо.ме[п-времени можно судить о паправлениидвижеття изображающей точки М, а вместе с те.м и о поведении соответствующей реальтюй системы.

это соответствует автоколе6а[П1ям, нужно исследовать их устойчивость, т, е. показать, что в пс])еходном iipoiiecce система ведет себя, как изображено на рис. 16.3. а, ио пе так, как на рис. 16..3, б. Это будет показано ниже.

Амплитуда найденных автоколебаний определяется как 0 ,., па участке АБ (рис. 16.5, а) путем исследования функции (16.15) па максимум обычным путе.м.

Фазовое пространство. Для наглядного представления о сложных нелинейных процессах управлеиня часто прибегают к понятию ([)азового пространства, которое .заключается в следую1цем. /Чифференциааьное уравнение замкнутой системы п-го порядка можно преобразовать к систе.ме п диффере1П1иа;П)Пых уравнений первого порядка в виде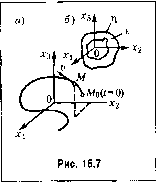

Начальные условия (х,о, Xoq, Х30) определяют координаты начальной точки фазовой траектории Mq (рис. 16.7, а) Если пе1)еменных в уравнениях (16.21) будет всего две-X, и Х2 (система второго порядка), то изображающая точка будет двигаться не в пространстве, а на плоскости (фазовая плоскость).

Если переменных будет любое число и > 3 (система п-го порядка), то фазовое пространство будет пе трехмерным, а п-.мерпым.

Итак, фазовое пространство и фазовые траектории представляют собой лищь геометрический образ процессов, протекающих в систе.ме. В это.м геометрическом представлении участвуют координаты и исключено время. Фазовая траектория сама по себе дает лишь качественное представление о характере гюве-депия системы. Чтобы определить количественно положение изображающей точки (а значит, и состояние системы) в любой .чю.мент вре.мени, нужно найти peineime заданных дифференциальных уравнений (16.21) во вре.мени.

Если уравнения (16.21) составлены в отк.юпениях от установившегося состояния, то последнее характеризуется значениями, =Х2=... = х = 0. Следовательно, изображением устагювившегося состояния системы является начало координат фазового пространства.

Отсюда вытекает, что фазовые траектории устойчивой линейной системы будут асимптотически приближаться к иача-чу координат при неограгщченном увеличении вре.мени. Фа.зовые траектории неустойчивой линейной системы будут неограниченно удатяться от начала координат.

Для нелинейной системы вследствие ряда особенностей процессов, отмечавшихся выше, фазовые траектории могут принимать са.мые разнообразные очертания. Если имеется аси.мптотическая устойчивость для определогпого круга начальных условий, то все фазовые траектории, которые начинаются внутри определенной области т), окружающей начало координат фазового прострачютва (рис. 16.7, б), будут асимптотически приближаться к началу координат. Если устойчивость неасимптотическая, то фазовые траектории, начинающиеся внутри области т) могут иметь любые очертания, но не будут выходить за пределы некоторой определениой области е, окружающей начало координат (рис. 16.7, б).

Формулировка понятия устойчивости по Ляпунову. Иевозмуидеиное движение (установивнгийся процесс) называется устойчивым, если при заданной сколь угодно малой области е (рис. 16.7, б) можно найти такую область т), что при начальных условиях, расположенных внутри .этой области, возму]цеп1юе движение (переходный процесс) будет таким, что изображающая точка не выйдет из области е при любом сколь угодно большо.м значении времени t (см. § 6.1).

В аналитической записи формулировка понятия устойчивости по Ляпунову будет следующей. Иевозмущеиное движение (устаповивнпгйся iipoiiecc) будет устойчи-вы.м, если при заданных положительных сколь угодно малых числах е,- можно наити такие положительные числа т,- (г = 1,..., п), что при начальных условиях

.г,о<л,- (г=и...,п) (16.22)