J г

Rix) = х{1:)х(с + т) = lim- J x(L)xit + x)dt,

R(x) = \x(t)-x]\x(t + x)-x\=\m- [x(t) - x]\x{t + т) -x\dt.

(11.51)

Для стационарного П1юцссса корреляционная функция определяет зависимость, случайной величины х в последующий момент времени L + х or предществуюн1его значения в момент t:

Рассмотрим основные свойства корре.тяииоииых функций.

1. Из определения коррелящюнной функции (11.46) и (11.47) следует свойство симметрии: R (t, f,) = R (f t) и (t, г,) = ff (f f)-

2. При t = корреляционная функция R (t, i,) дает средний квадрат случайной величины, а R (t, г,) - дисперсию:

RitJ.) = M\x-(t)] = ?(0, R\t,t) = M\{x(t)-x(t)f\ = D(t).

3. Можно показать, что прибавление к случайны.м величинам произвольных неслучайных величин не .меняет их корреляпиоИ1ЫХ .моментов и дисперсии. Поэто.му корреляционная функция Rf (Л i) не изменится, если к случайной функции добавить произвольную неслучайную функцию. Это свойство не относится к функции R (с, f,), так как добавление неслучайных величин к случайным изменяет начальные .моменты. В этом случае корреляционная функция будет равна сумме корреляционных функций случайной и неслучайной функций.

Иногда в рассмотрение вводится нормированная корреляционная функция

p(t,tO= . . (11.49)

Аналогично корреляционной функции .можно ввести понятие взаимной корреляционной функции для двух случайных величин х (() и у (t):

R,(t,t,) = M\x(t)y(t)l R!i.yit,t,) = M[{x(t)-x(t)){y(t,)-y(t)}]. (11.50)

В случае тож;тественпого равенства пулю взаи.мной кор[)еляпио1пюй функции случайные функции,г (/.) и у (t) называют некоррели]юва11ПЫМи.

EcjTh взаимная корреляционная функция отлична от нуля, то.г (/) иг/ (t) носят название коррелированных случайных функций.

В случае стационарности процесса корреляциошпяе функции R {t, t) и /? (t, г,) не будут зависеть от текущего значения времени t и будут определяться только временным сдвиго.м т = г, - t.

С учето.м эргодичности стационарного процесса корреляционной функцией можно назвать среднее по времен и от произведения x(t)nx(t + т) или x(t) - х и x(t + x) - х

R{Q) = xXt)x(t) = x.

3. При т -> оо корреляционная функция дает квадрат среднего значения случайной величины. Докажем это. Па основании эргодической гипотезы

/?(т) = X(t)x(t -Н т) = j Xx2w2 (.г, ,.Г2,т)с/х, JXj.

При т -> оо величины .г, и можно считать независимы.ми. Отсюда, принимая во вниматше формулу (11.39) для независимых случайных величии, получим

/?(-) = J X, ш>(х, )dx \ x2w(x2 )dx2 =(xf= (xf.

4. Значение корреляционной функции ири т = О является ее наибольшим значением, т. е. имеет .место перавепство R(0)> R (т). Докажем .это. Рассмотри.м очевидное неравенство

[x{t)-x(t + x)f>0.

Сделае.м иреобразова)ше

х (t) + а!(С + т) > 2х (I) x(t + т).

Возьме.м теперь среднее но вре.мени от правой и левой частей. В результате получим:

х (О + x\t + т) = 2х = 2/?(0), 2x(t)x(t + т) = 2/?(т),

откуда и вытекает следующее неравенство: R{0)> R (т).

5. Значение корреляционной функции чан[е всего будет тем меньше, чем больше про.межутки времени т, так как связь .между далеко отстоящими друг от друга значениями X будет обычно слабее.

6. Чем менееишфциопеп (более подвижен) объект наблюдения, тем быстрее убывает R (т) с увеличением т. Например, у са.молета, как подвижной цели, связь .между последующими и предыдущими положения\ш (при задаином т) будет тем мещше, чем он легче и .мапеврепнее. Отсюда следует, что чем быстрее убывает корреляционная функция, тем более высокие частоты будут присутствовать в случайном процессе.

На рис. 11.14 в качестве нри.мера приведены две корреляцио1И1ые функции и две соответствующие им реализации процесса при одинаковых среднеквадратичных значениях случайной величины. Второй процесс по сравнению с первы.м и.меет более тонкую структуру, т. е. в нем присутствуют более высокие частоты.

Приведем основные свойства корреляционной функции стационарного процесса применительно к величине R (т).

1. Корреляционная функция является четной функцией, т. е. R (--т) = R (т). Это вытекает из са.мого определения корреля)1ионной функции.

2. При 1 = 0 корреляционная функция дает средний квадрат случайной величины: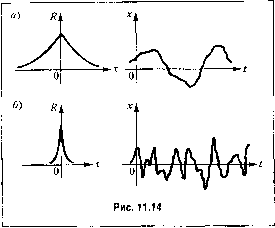

Таким образом, при известной корреляциопной функции легко определяются следуюпи1е вероятностные характеристики:

а) среднее зпанение (момент первого порядка)

i = x = 7 W;

б) среднеквадратичное значение (момент второго порядка)

?=?=/г(0);

в) дисперсия

D = Я (0) - й (-);

i) среднеквадратичное отклоните

a = R(0)-Ri).

Корреляционную функцию можно найти па основании экспериментально снятой кривой случайного процесса при наличии достаточно длительной записи (рис. 11.15). Обработка имеющейся осциллограммы прои.зводится следуюпш.м образо.м. Весь интервал записи осциллограммы Г делится па Травных частей, длительность которых составляет

ас = t/N.

Затем для различных значений т = mAt находятся средние значения произведений ординат:

N-m ±

T=NM

По эти.м значениям строится график корреляционной функции в зависимости от интервала т или времени т = тА1.

Корреляционную функцию можно найти по результатам эксперимента также при

помощи специальных приборов - корреляторов, которые автоматически вычисляют среднее произведение двух ординат осциллограммы, отстоящих друг от друга на расстояние т.

Если найденная корреляционная функция R (т) содержит постоянную составляющую X = yJR{°°), то, выделив ее, можно перейти к корреляциопной функции R° (т) в соответствии с (11.48), т.е. Vt)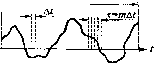

R(T)-(xf.