у=рх

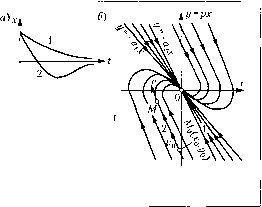Рис. 16.11

На рис. 16.11, а показаны два воз.можных варианта (кривые 1 и2) протекания такого процесса. Легко видеть, что на фазовой плоскости (х, у) это изобразится кривыми 1 и 2 соответственно (рис. 16.11, б), так как в пер-BO.VI варианте все время х > О и г/ < О, а во втором варианте знаки х и у .меняются по одному разу. Границы областей 1 \i2 представляют собой прямые у = ~ахну = -аз-г, получающиеся из уравнений (16,27) соответственно при ttj = О и при а, = О (обращение одного из корней в нуль).

В отличие от прежнего здесь все фазовые траектории вливаются непосредственно в начало координат О фазовой плоскости. Однако изображающая точка Мне попадает в начато координат в конечное время, а приб.тижается асимптотически.

Итак, затухающи.м апериодическим процессам в системе отвечают фазовые траектории, вливающиеся в начало координат.

С л у ч а й 5. Этот случай (вещественные положителыпле корни) соответствует также апериодическому процессу, определяемому теми же уравнениями (16.27), по при а, < О и а.2 < 0. Аналогично предыдущему получаем кривые процесса и фазовые траектории, изображенные нарис. 16.12.

Случай 6. В этом случае (вещественные корпи разных знаков) также имеет место апериодический процесс (16.27) (рис. 16.13,а), гдеа, иа2 и.меют разные знаки, но картина фазовГ)1х траекторий здесь иная. Так как а2 < О, то введем обозначение а = -а2, приче.м для простоты построений рассмотрим случай а, = 0. что соответствует

dy 2 п

согласно (16.23) уравнению системы *~0 и согласно (16.2э) - уравнению

фазовых траекторий

б) у-рх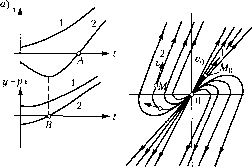

dy 2 X - = а-. dt у

(16.28)

Интегрирование последних аналогично случаю 1 дает

2 . 2

= 1, т. е. семейство ги-

(aCf

иербол, изображенное па рис 16.13,6.

Нан равлен и я ДВ иже н ия изоб-ражающей точки М по фазовым траектория.м, показанные иа рис 16.13, б, легко определяются в

каждой четверти плоскости по знаку dy/dx (\6.28).

Аналогичная картина фазовых траекторий получится в данном случае и при 0.

Итак, расходянитмся апериодическим процессам в системе отвечают фазовые траектории типа рис. 16.12, били типа рис. 16.13,6, приче.м изображающая точка, двигаясь по ним, в конечном итоге удаляется от начала координат.

Особые точки. В точках, которые соответствуют установившемуся состоянию, получаем согласно (16.25) неопределенное выражение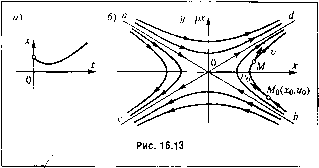

dx- - 0

т. е. пеопределейное направление касательных к интегральным кривым (фазовым тра-ектория.м). Такие точки называются особыми точками, приче.м для них существует следующая класспфикапия:

а) особые точки типа точки О на рис. 16.8, б называются центрами,

б) особые точки типа рис. 16.9, 6 называются устойчивыми фокуса.ми,

в) особые точки типа рис. 16.10, б11азываются пеустойчивы.ми фокусами,

г) особые точки тина рис. 16.11, 6 называются устойчивыми узлами,

д) особые точки тина рис. 16.12,6 называются неустойчивыми узлами,

е) особые точки тина рис. 16.13,6 называются седлами (сед;ю всегда неустойчиво).

Особые линии для нелинейных систем. Реальные систе.мы авто.матического унрав-ле1П1я можно считать линейными чаще всего в предположении .малости отклонений переменных от их значений в определенном установившемся состоянии.

За пределами указанной области вследствие зпачите.чьпого отклонения характеристик от линейных картина фазовых траекторий может сильно из.мениться и стать качествеппоиной.

В частности, если по линейной теории система оказывается неустойчивой и процесс начинает расходиться, то может оказаться, что из-за фактической нелинейности характеристик он не будет расходящимся неограничепно. Амплитуда расходящихся колебаний может увеличиваться только до определенного значения, а .затем оставаться постоянной, т. е. неустойчивая линейная авто.матическая система как бы превращается в устойчивую нелинейную автоколебательную систему (система 1е11ерирует устойчивые колебания онределенгюй фор.мы).

Картина фазовых траекторий для такой систеМ1> изображена на рис. 16.14, а. .Здесь вблизи начала координат получаются спирали, как в неустойчивой линейной системе (рис. 16.10, б), но далее все они расходятся не до бесконечности, а приближаются

асимптотически к некоторому за\п<нутому контуру ограниченных рааме1)ов, как показано на рнс. 16.14, а. К нему же приб,.чижаются и все спирали, находящиеся вне контура. Это соответствует картине п1)оцессов во времени, изображепгтой па рис. 16.3, а. Такого вида замкнутый контур, П1)едставля[0-щий собой наиболее важный для теории тип особг>1хлипи11 на фазовой плоскости, 1К1зы-вается устойчивы.м П1)едель-иым циклом.

Устойчивый предельный цикл соответствует автоко-лебания.м системы. Размеры предельного цикла А и В (рис. 16.14, а) представляют амплитуды колебаний самой величины X и скорости ее

У = . Для

оиредслепия периода автоко-лебаиий надо об1)атиться к рси1епию уравиеиий во времени.

С.тучаю устойчивости систе.мы в .малом и пеус-

тойчивости в бо.тьшом (рис, 16.3, б) соответствует картина фазовых траекторий, и.зображеииая нарис. 16.14, б. Грагпша начальных условий, до которой система устойчива, имеет чаще всего па фазовой плоскости вид неустойчивого предельного гшкла, как на рис. 16,14, б, от которого в обе стороны удаляются спиралевидные фазовые траектории. Это - втор(Л1 важны!! тип особых линий, онределяюпцгй устойчивость системы в малом и неустойчивость в бо;плиом .

Замети.м, что в этом случае .может быть также еще более удаленный устойчивы!! предельный цикл (рис. 16.14, е), соответствующий автоколебапия.м с большой амплитудой. Это соответствует процессам во времени, изображеппым па рис. 16.3, гЛ акие же припципиа7гьиые качественные изменения картины фазовых траекторий при достаточно больших отклонениях могут наблюдаться и в случаях апериодических иропес-сов (рис. 16.12, б и 16.13, б), вк.;1ючая превращеипя их в колебательные и наоборот. Например, картине процессов во времени, показаппой иа рис. 16.3, в, соответств.ует картина фазовых траекторий па рис. 16.14, е.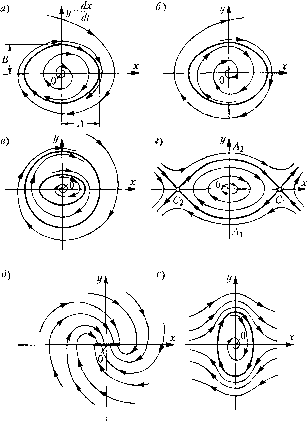

Рис,16.14

изменения