Аналогично для системы, паходяп1ейся согласно линейной теории [[а границе устойчивости (при чисто м1н1мых корнях), картина фазовых траекторий, изображенная на рис. 16.8, б, может и.меть место лин1Ь вблизи состояния установившегося )ежи.ма О. При больнн1х отклонениях, если линейность характеристик звеньев систе.мы нарушается, картина фазовых траекторий будет другой. Один из воз.можных вариантов изменения фазовых траекторий при больших отклонениях в этом случае показан па рис. 16.14, г. Здесь, кроме особой точки О типа центра, появляются два седла С, и Q, что приводит фактически к неустойчивости системы. Но .может иметь место и устойчивый предельный никл. Особые линии такого типа, как C]AC2 и СггС, (рис. 16.14, г), па фазовой плоскости называются сепаратрисами (третий тип особых липни). Особые линии более сложного очерташгя рассматриваться пе будут.

Здесь говорилось пока о системах, которые при малых отклонениях рассматриваются как линейные. Но совершенно аналогичная картина получается и для таких нелинейных систем автоматического управления, которые даже в малом нельзя рассматривать как линейные. Таковыми являются многочисленные тины релейных систем, а также системы с зоной нечувствительности, с гистерезисной петлей, с сухим трепие.м, с зазором. Интересно отметить, что некоторые из таких систем скорее в большо.м , че.м в мало.м , могут приближаться к линейным, когда зона нечувствительности HJHi зазор оказ1>шаются малыми по сравпению с величиной отклонепийх.

В системах с зоной нечувствительности и с сухим треиие.м существуют, как известно, области застоя, когда установившемуся состоянию при данных внешних ус;юви-ях (данной нагрузке) соответствует не одна точка, а целая область возможных равновесных состояний системы. На фазовой плоскости .это выражаетс>< в то.м, что особая точка вытягивается в особый отрезок (рис. 16.14, д).

Заметим, наконец, что координатами (х,у) фазовой п.тоскостп могут служить пе обязательно отклонения управляемой величины и скорость ее, как бььчо вьпне. Для этой цели .могут быть взяты любые две не)еме?[щ)1е, однозначно характеризуюпше состояние системы второго порядка в произво.тьпый момент времени.

Пример. Изобрази.м па фазовой плоскости переходный процесс и автоколеба-ния.в системе стабилизации температуры, рассмотреппой выше. Координаты фазовой плоскости будут-

х=е и y-f. (16.29)

Если г/ > О, то coiviacHo (16.10) и рис. 16.4, а переключение управляющего устройства происходит П1)И 9 = +й(линия EF па рис. 16.15); если же г/<0, то при 0 =-Л (линия GH). CiipaBa от линии переключения £ГСЯ справедливо ураВ1гение системы (16.12), а слева-(16.13).

YpaBHetHie (16.12) в обозначениях (16.29) примет вид

dx dy ,

откуда гюлучаем дифференциальное уравпеппе фазовых траекторий

= 1-А£ (16.30)

dx Г, 1\у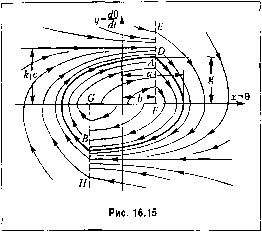

вает при у<0.

Уравнение (16.13) в обозначениях (16.29) будет

dx 7j 1]у

Интегрирование его дает X = ,сГ, Ь\у + ксI - Ту + С, (16.31)

где С] - произвольная постоянная.

Каждому конкретному значению С, соответствует определенная кривая на фазовой плоскости. Семейство кривых, отвечающих ра,зличпым значепия.м C, и.зображепо на рис. 16.15 справа от линии EFGU. Эти кривые имеют асимптоту г/= с. Направление движешгя изображающей точки по ним, показатпюе

стрелка.ми, определяется из условия

У = -7-, т.е.х возрастает при г/ > О и убы-dt

(16.32)

что дает решение

х= -кусТ \п\у -к,с\ - 1\у + С2,

согласно которо.му наносится семейство фа,зовых траекторий слева от линии FA-GII (рис. 16.15).

В результате получится, что фазовые траектории расходятся от начала координат и сходятся из бесконечности, т. е. имеет место случай, аналогичный рис, 16,14, а, а значит, где-то должен быть устойчивый предельный тщк-т. Он обозначен жирной линией нарис. 16.15.

Следовательно, в данной системе будут наблюдаться автоколебания, к которым сходится переходный процесс с обеих сторон, т. е. при любых начальных условиях.

Автоколебательный ироцесс является здесь едииственно возможным видом установившегося процесса, а строгое иоддержапие постоянной температуры (0 = 0) певоз-.можно. А.мплитуда автоколебаний температуры в данной систе.ме изображается па рис. 16.15 отрезко.м а. Период же автоколебаний определяется решением уравнений во времени, как было сделано выше Половины АВ и BD (рис. 16.15) предельного никла соответствуют полупериодам АВ и BD (рис. 16.4,6) автоколебаний.

Отрезок g (рис. 16.15) изображает амплитуду скорости и.змепеиия температуры при автоколебаниях; зго есть величи1ш (16.18). Видно, 4T0g< А,с.

Перейдем к составлению уравнений нелинейных систем автоматического управления.

§ 16.2. Уравнения систем с нелинейностью релейного типа

Следуя сделанным в § 16.1 замечания.м, приведем несколько примеров составления уравнений нелинейных систем релейного типа.

Система автоматической стабилизации напряжения. Пусть имеется генератор постоянного тока (управляемый объект) с вибрационны.м регулятором напряжения. Упрощенная принципиальная схема такой системы показана на рис. 16.16.

Когда контакты К под действием пружины П замкнуты, резистор, обозначенный через 2г1, выключен из цепи возбужде1тя генератора 1. Систе.ма рассчитана так, что при этом нанряже1гие Опаклем.мах генератора возрастает. В результате увеличивается ток /2 в обмотке 2 .электрома1ттитного реле и якорь реле притягивается, размыкая тем самым контакты К. При разомкнутых же контактах К в цепь возбуждения включен резистор 2г,. Это вызывает снижешге напряжения U, а 31гачит уменьпюние тока /2 и отпускание реле, в результате чего контакты К снова замыкаются, выключая тем самым резистор 2г1 из цепи возбуждения. Настройка системы на желаемое номинальное значение управляемой величины {/производится установкой резистора /?д.

Уравнение объекта (генератора) представим в линейном виде:

(7\p+l)AU=-kAr + f(t),

(16.33)

где Ar- изменение сопротивления цепи возбуждения (управляющее во.злействие); постоянная вре.мегнг 7\ и коэффициент ki опредешются параметра.ми якоря и tienn возбуждения.

Уравнение чувствителыгого элемента (об.мотки .электромагнита 2) запишем в виде

(T2P+l)Al2 = k2AU.

(16.34)

Начало отсчета величин отклонений AU, AI2 и Аг будет определено ниже.

Управляющий орган (контакты К, скачком включающие и вьпочючаюннте резистор 2г,) является нелинейным звеном релейного типа. Выходная величина его - сопротивление г цени возбуждения - меняется скачкообразно при срабатывании и отпускании реле, т. е. в зависимости от величины тока I2 в цепи обмотки 2 электромагнитного реле. Это изображено на рис. 16.17, а, где 4р и 4.,. - токи полного срабатывания и отпускания реле. Для составления уравнения такого нелинейного звена удобно, как

RuWi

К>

-U-*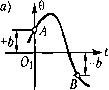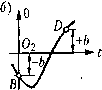