причем согласно CBoiicTBy (17.46) эта функция W, так же как и сама V, тождественно обращается в нуль нри Xj = Xj =... = х = 0. Поэто.му к ней в одинаковой степени можно применять все те же понятия зиакоопределенпости, знакопостояпства и зиакоперемен-ности в некоторой области вокруг начала координат, о которых говорилось выше но отношению к функции V.

Здесь ньча речь только об уравнениях (нелинейных), в которые не входит в явном виде вре.мя t, так как только этот случай будет рассматргиаться в дальнейшем. Вообще же метод Ляпунова может применяться и при наличии времени t в явном виде, в частности для уравнений с переменными коэффициеита.ми (линейных и нелинейных).

Вазируясь на этих предварительных сведениях, дадим оби1ую формулировку теорем Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость. Теоре.мы эти годятся для исследования устойчивости систем управлепия не только при .малых, по и при больищх откло1юниях, если для них справедливы исходные уравнения дайной систе.\П)1 управления. Устойчивость системы при любых больин1х начальных отклонениях называется коротко - устойчивостью в целом.

Теорема Ляпунова об устойчивости нелинейных систем. Теорема формулируется следуюнцгм образом: если при заданных в форме (17,45) уравнениях системы п-го порядка можно подобрать такую знакоопределенную функцию Ляпунова V (Xj, л-2 .., х ), чтобы ее производ)1ая по вре.иепи V/ (Xj, Х2,..., х ) тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива. Прн зиакоопределепной ([зункции Сбудет иметь место асимптотическая устойчивость.

Проиллюстрируем справедливость этой теоремы па наглядных геометрических образах. Д.1Я простоты возьмем систему третьего порядка (п = 3). Уравнения (17.45) для нее в общем виде будут

- = Х,(Х Х2,.Хз),

- = Х2(Х1,Х2,Хз), (17.51)

=Хз(Х Х2,Хз).

Возьмем знакоопределеттую положительную функцию Ляпунова в виде

V = ax+bxl + cxl (17.52)

где а,Ь,с - произвольно заданные вещественные числа.

Будем придавать величине Увозрастаюпще постоянные значения; 7=0, С С2, ..., что означает

a4f +bxi-\-c.xl=0, axf+hxl+cx=Ci,

ах} + fexf + cxl = C2,

Первое из этих выражений соответствует одной точке х, = = Хз = О (началу координат фазового пространства), а оста-ньные - поверхностям эл;пи1соидов в ({)азо-вом пространстве, причем каждый последуюннн! эллипсоид содержит внутри себя целиком предыдущий (рис. 17.10).

Возьмем теперь производную от функции Ляпунова по вре.мени. Согласно (17.49) и (17.52)

= 2rtx,X, (xi ,Х2 ,Хз) + IbxX (х, ,Х2 ,.Хз) + 2сХзХз(х, ,Х2 ,Хз) = W(x X2,X:i),

1-де функции А 2, Хз берутся из заданных уравнений системы (17.51).

Если полученная таки.м путем функция 1У(Х,Х2,Хз) окажется знакоопрсделенной отрицательной, т. е. если

dV

(17.53)

во всех точках исследус.\и)го фазового пространства, кроме одного только начала координат, где

dV dt

= 0 (npnxi = Х2 =Хз 0),

то при любых начальных условиях изображающая точка М (рис. 17.10) вследствие (17.53) будет двигаться в сторону уменьпения значения V, т. е. будет пересекать эллипсоиды, изображенные па рис. 17.10, извне внутрь. В результате с течением времени изображающая точка М будет cтpeцтьcя к началу координат О фазового прост])ап-ства (аси.\цгготическая устойчивость) и уже никак пе сможет выйти за пределы тех эллипсоидов, в которые она прогнкла.

Это и означает затухание всех отклонений х Х2, Х3 в переходном процессе с течением времени. Таки.м образом, установлена устойчивость данной систе.мы, что иллюстрирует справедливость теоремы для системы третьего порядка (в случае знакоопре-деленной функции W).

Отсюда вытекает справедливость теоремы и в обп1ем случае. Рассужде1гия остаются аналогичными, только в.место трех уравнений (17.51) будет п уравпешш (17.45). Как и раньше, для любой зпакоопределенной положительной функнии Ляпунова У(х Х2.....х ) = Сполучим некоторыезамкнутьн поверхности, ок1)ужаюище начало координат (рис. 17.10), но уже не в обычном трехмерном, а в и-мерпом фа.зовом пространстве (их иногда называют гиперповерхпостя.ми).

Поэтому, если производная= 1У(Х,Х2,...,х ) ока-от

жется знакооиределеппой отрицательной, то траектория изображаюн1ей точки М в и-мерном пространстве при любых пачальп1>1х условиях с течением времени будет пересекать указанные поверхности только извне внутрь, что и свидетельствует об устойчивости даппой системы.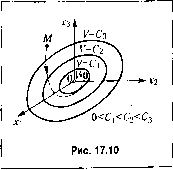

Если же функция Побудет ие знакоопределенной, а зиаконостоятюй, то очевидно, что траектория изображающей точки Мне везде будет пересекать поверхности V= С, а может их касаться в тех точках, где обращается в нуль (помимо начала координат). Но так как во всех других местах фазового пространства функция иимеет один и тот же знак, вследствие чего изображаюигая точка может идти только извне внутрь поверхности V = С, то при ренюнии задачи остается только проверить, пе застрянет ли изображаюпшя точка та.м, где W=0 (см. пример ниже).

Замечания к теореме Ляпунова об устойчивости. 11о поводу сформулированной теоремы Ляпунова об устойчивости системы необходимо сделать следующие два важных замечания.

1. В теоре.ме речь идет о подборе функции Ляпунова V (х лз,..., х ). Всюбще говоря, нри заданных в форме (17.45) уравнениях системы управления .можно подобрать несколько различных вариантов функции V, поскольку требуется только зпако-онределенпость ее и ее производной. Ра.зличные варианты функщт V, удовлетворяющие теореме, могут дать соответственно различные варианты условий устойчивости для одной и той же систе.мы. При это.м одни из них будут птре, другие уже, последние могут входить в первые как частный случай и т. д.

Поэто.му, BoooHie говоря, данная гсоре.ма Ляпунова обеспечнвает иолучепне достаточных условий устойчивости, которые не всегда будут и необходимыми, т. е. нри выполнении условий теоремы система наверняка будет устойчивой, но эти условия могут не охватывать всей области устойчивости системы но параметра.м. В самом деле, если выбрана функция V, удовлепюряющая теореме, пет уверенности в то.м, что нельзя подобрать другой вариант функции V, который бы еще более полно охватывал область устойчивости данной системы.

Геометрически .это значит, что, получив определенное семейство пове()хиостей V = С (рис. 17.10) и убедивпшсь, что траекго()Ии изображающей точктг М приближаются к началу координат, пересекая эти поверхности извне внутрь, нельзя бытьуве()еппым в том, что пе существует еще других вариантов траекторий изображающей точки М, которые в отдельных местах .могут пересекать данные поверхности изнутри вовне, но все же с течением времени в конце концов неограниченно приближаться к началу координат. Такие траектории будут соответствовать другому семейству поверхностей V- С, т. е. другому варианту выбора функции Ляпунова.

В ряде технических за/дач можно вполне удовлетвориться этими достаточными условиями устойчивости. От более или менее удачного подбора функпии Ляпунова V будет зависеть большая или меньшая близость полученных достаточных условий устойчивости к необходимым и достаточным, т. е. более или менее полный охват всей области устойчивости данной систе.мы. Существуют, конечно, итакиефу1и<ции К(лГ, Х2,...,.г ), которые соответствуют всей области устойчивости.

2. К сформулированной выше теореме Ляпунова необходимо добавить, что понятие устойчивости по Ляпунову допускает, чтобы при знакоопределенной функции V производная от нее Wбыла не обязательно знакоопределенной или знакопостоянной, а могла быть и тождественно равна нулю во всем рассматриваемом фазовом пространстве. В это.м случае, проводя аналогичные прежни.м рассуждения, легко убедиться, что изображающая точка М (рис. 17.10) будет оставаться все время на какой-нибудь одной из поверхностей V= const, куда ее забросили начальные условия. В ре.зультате