а)£0 с

б) Я k 1,0

/; Ри I -const

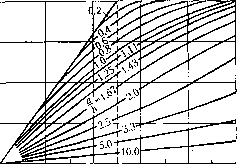О 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0

ири -const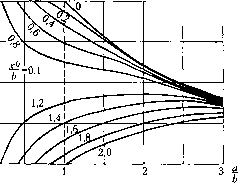

Рис. 19.13

f-kx.

Из графиков для f (рис. 19.13, я) видно, что ири наличии колебаний входной величины не;ин1ейноп) звена его статическая характеристика для медленно меняюн1е1Х)ся воздействия (функция смещения) сглаживается, причем увеличение амплитуды колебаний входной величины приводит к уменьшению коэффициента усиления пелицеЙ1К)Го.звена по постоянному или медленно меняющемуся входному воздействию.

Графики для q (рис. 19.13, б) характеризуют прохождение через нелинейное звепо колебательной составляющей в зависимости от амплитуды на входе и смещения центра колебаний. Как видно, увеличение смещения приводит к уменьшению коэффициента усиления ДJTя колебательной составляющей.

Нелинейная характеристика типа люфта или зазора. В случае несимметричных колебаний нелинейная характеристикатипа люфта или за.зора (рис. 19.14) смещается вдоль средней линии, так что ее прежний центр О переходит в по;южение СУ. Постоянная состав-ляюи1ая в это.м случае определяется простой формулой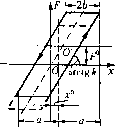

Рис, 19.14

Колебательная составляюн1ая функции f (х + а sin V;) отпоситстьно нового центра колебаний пе зависит от величины с.меп1епия х . Так, например, зубчатая пара, имеющая люфт, передает движение с те.м же передаточным число.м для любых углов поворота ведущей шестерни, В случае колебаний в кинематической передаче, включаюпюй данную пару, люфт будет проявлять себя одинаково для любых углов поворота. Поэтому для коэ(х})ициентов гар.мошгческой линеаризации характеристики типа люфта или зазора в случае смешенного центра колебаний относителыю начала отсчета будем иметь те же (}зормулы (18.27), что и для случая симметричных колебаний.

Глава 20

ОЦЕНКА КАЧЕСТВА

НЕЛИНЕЙНЫХ ПРОЦЕССОВ УПРАВЛЕНИЯ

§ 20.1. Приближенное исследование колебательных переходных процессов

Рассмотрим симметричные относительно оси времени колебательные переходные процессы в нелинейной автоматической системе, которые в первом грубом приближении .могут быть описаны затухающей или расходящейся синусоидой с .медленно мепя-юннгмися во времени показателем затухания и частотой (рис. 20.1).

Прежде че.м записать это .математически, обратим внимание па два существенных обстоятельства. Для линейных систем, когда показатель затухания = const и частота О) = const, пинлут

х = %е sin(шг;-l-ф).

(20.1)

Если же частота ш и показатель затухания С, в процессе колебаний меняются с течением времени, то решение следует записывать в другом виде.

Во-первых, следует писать sin Ц1 (t.) и определять текущее значение частоты в произвольный момент времени в виде

(20.2)

причем

(20.3)

гден/() - постоянная (начальнаяфаза). СуП1есгвуетдругой способ, когда полагают у = со + ф() при Шо = const, причем согласно (20.2) текущее значение частоты

dvf dw

с0 = -7 = 0)0 +-

(20.4)

Однако в данной задаче целесообразно придерживаться первого представления ((20.2) и (20.3)).

Во-вторых, при переменном во времени показателе затухания следует определять текущее значение а.милитуды а (рис. 20.1) пе в виде аце, как сделано в (20.1), а в виде дифференциальной зависимости

da

(20.5)

Тогда в случае линейной систелпя, когда С = const, получаем как частный случай

da . , г,

- = C,OT, а = аге , а

а в случае нелинейной системы, когда .меняется в процессе колебаний, текущее значение амплитуды согласно (20.5) будет

- = dt, a = aJ\ (20.6)

т. е. огибающая колебаний (рис. 20.1) состоит из элементарных отрезков экспонент с непрерывно меняюнтмся показателем С-

Итак, будем искать рещение для переходного процесса в нелинейной системе как первое приближение в виде

.t = asin4/, (20.7)

da dw

= С. со-. (20.8)

приче.м иско.мыми неизвестными будем считать медленно .меняющиеся величины и ш.

Показатель затухания может характеризовать быстроту не только затухания, но и расхождения колеба1ШЙ:

>0 нри >0; dt

<0 при <0,

(20.9)

т. е. положительным значениям показателя затухания С, соответствуют расходящиеся колебания.

Как уже было сказано, величины и ш считаются медленно меняющимися функциями. Однако поскольку цостоя1П1ые значения могут соответствовать в линейных системах как медленному, так и быстрому затуханию колебаний, то и медленно меня-юншеся значения С, могут характеризовать как те, так и другие процессы.

Формулы гармонической линеаризации нелинейности для рассматриваемого случая будут иметь некоторую особен?юсть по сравнению с нрежин.ми. В самом деле, если величина показателя затухания С, не мала, то, дифференцируя выражение (20.7) но времени как произведение двух функций, с учетом (20.8) находим

рх = am cos \if + аС, sin \if. (20.10)

Отсюда и из (20.7) получаем

sin4/ = -, cos\ = - = x. (20.11)

а am am am