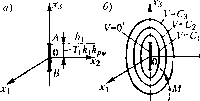0<С,<С2<Сз-

Рис. 17.13

Т. е. па.чичие гзоны застоя двигателя приводит к то.му, что в установившемся процессе курсовой угол .может принять любое постоянное зпачепие в пределах (17.65).

В новых переменных (17,61) установивнгийся процесс полета определяется значениями:

X, =0, х2=0,

(17.66)

чему соответствует любая точка отрезка АВ в фазово.м пространстве (рис. 17.13, а). При отыскании условий устойчивости рассмотрим два случая: у > 1 и О < у < 1. Случай у > 1. Возьмем функцию Ляпунова в виде

V--fxlxl.

/(л-з)а[гз.

(17.67)

Здесь интеграл будет всегда положительным, так как функция/(-з) нечетная (см. условие (17.54)). Поэтому Уесть знакоопределенная положительная функция, если у > 1, обращающаяся в нуль на отрезке установившегося процесса (рис. 17.13). Поверхности У(х .Г2, Хз) = С окружают этот отрезок (рис, 17,13, б), стягиваясь к нему с уменьшением С.

Состави.м производную от функции Ляпунова:

dV dV dx, dV dxn dV dx-, -. - =--L +--L +-.-1

dx Эх, dx Эх, dx

Эхз dx

причем частные производные возьмем из (17.67), а производные по безразмерному вре.мени - из уравнений системы (17.63). Тогда

W = -{y- l)xf + (Y- 1)х,/(хз )-ух2/(хз) + /(хз)[(Y- 1).г, + ух., - г/(хз)].

Представим .это в виде

W = -{y- 1)[/(хз) - X, 1 - (г - Y + 1)[/(Хз )]. (17.68)

Эта функция ТУзнаконостоянная, так как она не включает в себя координату Хз, а потому обрандается в пул ь не только на отрезке установившегося процесса АВ, а па всей полосе пнфиной АВ в плоскости Х2Х3 (рис. 17.13, в). Но вне .этой полосы согласно (17.68) она будет всюду отрицательной при

r>Y-l, еслиу>1. (17.69)

V=-xj+lxj + ]fix.,)dx,.

Производная от нее будет

W = = -{\-y)x,-rlf(x,)f.

Отсюда апалогич}Го предыдущему приходим к достаточному условию устойчивости системы в виде

г>0, если 0< Y< 1. (17.70)

Общий в ы вод. Полученные в данной задаче достаточные условия устойчивости (17,69) и (17,70) после подстановки выражений уи г через параметры системы (17,64) принимают вид соответственно

k , >0, если <Г,,

Поэтому согласно теореме Ляпунова об устойчивости выражение (17.69) является достаточным условием устойчивости рассматриваемой нелинейной систе.мы самолета с курсовым автопилото.м (при любой К[)ивизне и любом наклоне характеристики двигателя, имеющей вид рис. 17.12, б).

Траектория изображающей точки М будет пересекать поверхности V= С извне

внутрь везде, где W=<0. Нужно только проверить, не застрянет ли изображаю-at

щая точка Мтам, где обратпается в пуль (помимо отрезка установивп1егося процесса АВ). В данном случае речь идет о том, ие останется ли изображающая точка на полосе (показашюй на рис, 17.13, е), где W= О, если она случайно на нее попадет.

Для решения этого вопроса найдем проекции ско[)ОСти изоб[)ажающеп точки

dx, сЬ.) dx., -

М---когда эта точка находится в любом .месте указанной полосы. По-

dx dx dx скольку там

то искомые проекции скорости согласно (17.63) будут

dx, г\ dx.) . dxo

Таки.м образом, если изображающая точка М попадет на указанную полосу вне отрезка АВ (рис. 17.13, в), то она пе останется в ней, а пройдет ее поперек по пря.мой, па1)аллель}1ой оси х, с постоянной скоростью, равной ух2 как показано стрелками на рис. 17.13, е. Пройдя полосу, изображаюп1ая точка снова будет пересекать поверхности v С извне внутрь, т. е. данная систе.ма управления будет устойчивой.

Случай О < Y < 1- Д-я этого случая возь.мем функцию Ляпунова в виде

Первое из этих условий устойчивости говорит о том, что иередаточиое число обратной связи надо сделать достаточно больи,1Им, если производная рм введена в алгоритм управлепия пед9Статочно иитеисивпо. Из второго же условия устойчивости следует, что система будет устойчива при любой обратной связи, если не[)едаточное число по производной достаточ1Ю велико.

Как видим, данные условия устойчивости ие .зависят от формы характеристики двигателя (рис. 17.12, б), т. е. они одинаковы нри любой кривизне, любо.м наклоне и любой зоне застоя (в том числе и при однозначной релейной характеристике двигателя иостояппойч:корости, а также и ири линейной характеристике). Такие условия называются условиями абсолютной устойчивости. Они гарантируют, что при их выполнении систе.ма будет наверняка устойчива нри любой нелинейности с ограничением лишь (17.54). В действительности же система может быть устойчивой и в некоторой области за пределами этих условий устойчивости при конкретно заданной форме пе-.минейиости (см. гл. 18).

Пример учета нелинейности измерителя управляемой величины. На основании вышеизложенных теорем Ляпунова М. А. Айзермап показал, что если уравпение систе.мы содержит не;1инейиость

dxo ~dt

= a2,.r, +a22X2+- + a2 x ,

= a ,x,+a 2X2+- + a x ,

(17.71)

где7 (х) - однозначная нелинейная функция, обрашаюшаяся в пуль ирих = О, а -любое целое число из 1, 2,.,., п, то для устойчивости систе.мы достаточно, чтобы для линеаризованной системы (17.71) ири замене f (х/,) = ах можно было построить функцию Ляпунова У, произ1Юдпая от которой 1Уявляется знакоопределенной отрицательной функцией при любом значении а в интервале а, < о < если кривая F(x,) лежит между прямы.ми F= а,д7; и7 =а2Х как изображено, например, нарис, 17.14, а.

Пусть, например, в прежтгей системе самолета с курсовы.м автопи.тото.м (рис.17.12, а) уравпение объекта имеет вид (17.55), привод руля имеетлипейпую характеристикурЪ = kU, но потенциометр чувствительного элемента / (измерителя управляемой величиш,! vj/) имеет нелинейную характеристику, в результате чего получается нелинейное уравнешю автопилота

/;5 = /-(V) + y W-M. (17.72)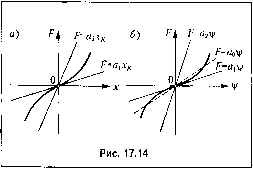