Решение первого из уравнений (14.75) можно получить как последовательно шаг за шагом, так и в за.мкнутой форме. В перво.м случае вычистителЬная процедура осуществляется следующим образом:

х({) = А*х(0) + Ь *м(0) + m*f(0); x(2):A*x(\) + b*u(i) + fn*f(\)\

(14.79)

Во втором случае, подставляя выражение для х(1) в выражение для х(2), выражение для х{2) в выражение для х(3) и т. д., получим

x(i) = iA*yx(0) + Y,(A*) ~ b*u(v).

(14.80)

Для простоты здесь положено, что /(г) = 0.

Решение (14.80) позволяет при известной последовательности u{i) пайти х(г) и,

следовагельгго, y(i) = cx(i) для любого наперед заданно1о .мо.меита времени / = iT.

Используя уравнершя (14.75), можно определить передаточные фуггкции рассматриваемой систе.\и>1. Для этого 1гайлем 2-преобразова1Н1Я от их левых и правых частей с учетом формулы (14.33) при пулевых нача/илН)1Х зпачеттях. В результате получим:

zX(z) - А * X(z) + h * U{z) + т * h\zy, Y{z)4{zy

(14.81)

X(2)=z{j(0} =

A, (2) 2(2)

(14.82)

Тогда

X{z) = {zE -A*y +b* U{z) + {zE-A*ym * F{zy

(14.83)

Y{z) = c\zE-A*yb*U{z) + c\zE-A*ym*F{zy

(14.84)

Таким образо.м, передаточные функтш системы определяются следующим обра-

зом:

W{z) = = c\zE-A*yb*;

(14.85)

Wf{z) = l\zE-A*ym*. (14.86)

Использование выражения (14.85) дает такой же результат, как и (14.58) при у< 1 или (14.60) при Y= 1. Передаточная функция (14.86) существует лишь присдела1гном ранее допущении о том, что воз.мущающее воздействие можно считать постояины.м на интервалах времени гТ< г< (г +1)Г.

§ 14.6. Устойчивость импульсных систем

В § 6.1 было показано, что непрерывная систе.ма устойчива, если все корнир (У = 1, 2,..., п) ее характеристического уравнения лежат в левой полуплоскости (рис. 14.8, а). При исследовании импульсных систе.м вместор используется новая переменная2= е. В теории фушсций комплексного перемешюго преобразования, в процессе которого од1га переменная заменяется некоторой функцией от новой переменной, а одна область комплексной плоскости отображается в другую, называется конформным преобразованием. Конфор.мное преобразовапие2 = е отображает левую полуплоскость плоскости р в область, ограниченную окружностью единичного радиуса на плоскости г (рис. 14.8,6). При ,зтом мни.мая ось плоскости р отображается в саму окружность.

Действительно, riycTbpi з = а ±;Р. Тогда

= еР) = e (cos pr±isin f,T). (14.87)

При этом j 2] 2! = С . Для значений а < О (что соответствует кориямр! 2 лежащим в левой полуплоскости нлоскостир) 12, 2I < 1, что соответствует корням, лежащим внутри круга единичного радиуса плоскости z. Если а = О, т. е. если корпир) 2 располагаются на мнимой оси плоскости/;, то корни г, 2 попадают па окружность единичного радиуса плоскости 2.

Таки,\1 образо.м, импульсная систе.ма устойчива, если все корпи ее характеристического уравнения лежат внутри круга единичного радиуса, т. е. если 12, < 1, v = 1,2, п, что совпадает с результатом (14.14). Если хотя бы один корень лежит вне круга единичного радиуса, то система неустойчива.

Окружность единичного радиуса представляет собой границу устойчивости для и.мпульсной системы.

Система находится на апериодической границе устойчивости, если в ее характеристическом уравнении

ао2 +а,2 +...+ = О (14.88)

и.меется корепь2 = 1, а остальные корни ])аснолагаются внутри круга единичного радиуса (рис. 14.8, в). В это.м случае переходная составляющая решения разностного уравнения (14.12) стечением времени стремится к значению C{z) = С.

Если в характеристическом уравпепии имеется пара комплексных сопряженных корней, расположенных на окружности единичного радиуса (рис. 14.8, г), т. е. таких, что Re 2 .ц -1- 2 v+i = 1. то имеет место ко.тебательная i-раница устойчивости. В этом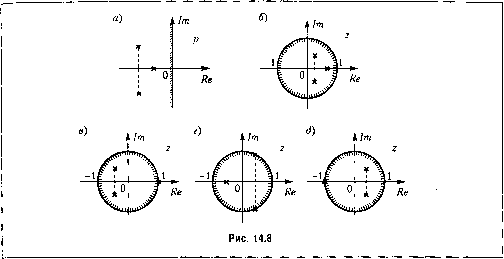

случае с течением времени в системе устанавливаются незатухающие периодические колебания. Вещественная часть указаниях корней Re z.v+i может быть положительной, как на рис. 14.8, г, отрицательной или нулевой.

Типичной для импульсных систем является так называемая граница устойчивости третьего типа, которой соответствует па.П1Чие в характеристическом уравнении кор1гя 2,= -1 (рис. 14.8, д). В этом случае в системе с течением времени устанавливаются незатухающие периодические колебания с периодом, равным 2Т, так как составляющая решения (14.12) С,(2,) = Q(-1) при изменении / нослеловательно припи.мает значения Q и - С,.

В §14.4 отмечалось, что обычно для оценки устойчивости и качества импульсных систем иснолызуются передаточная функция разо.мкнутой системы W(z) и передаточные функции замкнутой системы Ф(2) или 0.(2). Тогда в соответствии с выражениями (14.64) или (14.65) .характеристическое уравнение .замкнутой системы (14.88) может быть 1К)лучено следующим образом:

1 + W(z) = В(г) + С(2) = О,

(14.89)

где B(z) и C(z) - полиномы числителя и зна.менателя передаточной функции W(z).

Как правило, такое же уравнение получается и при использовании модифипиро-ваипой передаточной функции замкнутой системы Ф(2, е), определяемой по формуле (14.67). Лишь в отдельных редких частных случаях полипомы зна.менателей передаточных функций Ф(2) и Ф(2, е) могут иметь различное число корней fSOj. Эти случаи здесь ие рассматриваются.

Исследование устойчивости импульсных систем представляет собой более сложную задачу, чем исследование устойчивости непрерывных систем. Это связано с тем, что рассмотренные в главе 6 критерии устойчивости, такие как критерии Гурвица или Вышпеградского, устанавливают принадлежность корней характеристического уравнения к левой полуплоскости плоскости р, тогда как для устойчивости и.мпульсной