<0,

V да

>0,

1Эш,

<0,

, Эй)

<о.

то критерий (18.63) выполняется. Поэтому найденное периодическое реп1ение устойчиво. Следовательно, квадратичное трение приводит к автоколебания.м в той области пара.метров, где система без этого добавочного трения была бы неустойчивой. Это объясняется усилением лемпф11руюп1его действия квадратичной силы трения при увеличении амплитуды (и скорости) колебаний, что препятствует неограниченному раскачиванию систе.мы. Заметим, что переход закона сопротивления движению объекта от липейпо1-о к квадратичному при больп1их скоростях отражает реальные явления.

Л.\П1литуда и частота автоколебаний определяются здесь графико.м рис. 18,17, 6 или формула.ми (18.92), причем амплитуда колебаний угла 3 будет а = <я /а) .

Пример 4. Пусть в той же следяи1ей системе требуется учесть влияние зазора в меха1Н1ческой передаче между двигателем и унравляе.мы.м объектом (схематически он показан на рис. 16.20) ири линейной характеристике двигателя и при линейном трении. В колебательных процессах, которые .здесь рассматриваются, зависимость между угла.ми поворота (3 (после зазора) и (3, (до зазора) будет иметь нелинейный вид, показанный на рис. 16.20, б, где h - полови1Ш ширины за,зора. Кроме этой нелинейной .зависимости здесь присутствует вторая пелпнейпость (16.54). Полагая, что момент инерции управляемого объектау, велик по сравнению с приведенным моментом инерции двигателя, будем считать в. уравнении (16.54) Г,= 0.

Первая иелипейпость (рис. 16.20, б) после гармонической линеаризации ири Р a.sincofcor.Tacno формуле (18.30) припи.мает вид

(18.93)

где q {а) и q (а) определяются по фор.мулам (18.27), в которых надо считать к = 1 (так как характеристика рис. 16.20, б имеет наклоь[ 45°), а и.менно:

<? = -

Л 1 .

\j/i+- + -.sin2i/,

, \ 2

q =-CO.S ij/j = - л па

(18.94)

причем

Граничные значения о) и к совпадают здесь с прежними (18.88), но они соответствуют уже не (Я = о , а а = 0. В результате получаем график для определения амплитуды и частоты периодического решения, изображенный па рис. 18.17,6.

Поскольку здесь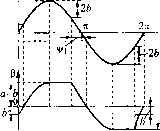

Рис. 18.18

Вторую нелинейность (16.,54) запишем ввиде/ (р2393) = г

Она подвергается гармонической линеаризации но фор.мула.м (18.11) также нри 3, = asin Ш.

Зависимость .между углами (3, и (3 показана на рис. 18,18. При этом из нижнего графика и из формул (16.54) видно, что

F(p2p pp,)=7>2p,+;;p,

71 Зл

0<\i<-, л-ч/,<ч/<-,

2л-\Г, < 1;/<2л

и (учитывая, что 7, = 0)

л Зл

- <\;<л-\1; -<¥<2л-\/,.

Условие отсутствия постоянной составляющей здесь выполняется, а Т1)етья из формул (18.11) принимает вид

<7,(а,(о) =

(acocosv;/)cos\j; (7v/ + Т{-а{У sin\j;)cosv/ й?\(/ +

T(j(-aw sinv/)cosv/(7\/+ 7o(-a(o sin\j/)cos\j/(7v/

аналогично определяется и (a, со). Произведя интегрирование и сравнив результаты с выражениями (18.94), получаем

(а,м) = м- ,?(а)7>2,

где q (а) то же, что в формулах (18.94).

В результате вместо нелинейного уравнения (16.54) при Г, = О имеем

[<72 (а) 7> + 1 - 9 (а) Гш] /?р, =

(18.96)

л 1 .

Vi+---sin2x/,

причем q {а) и\;, тсжс, что и в (18.94) и (18.95). На рис. 18.19,(2 и.зображепы графики для величии коэффициентов q (а), f/,((7), (72(a).

На основании (18.93), (18.96) и линейной части (16.53) приходим к характеристическому урав11епию

(Т,Р +1)[?2 (а)Т,р + 1- qXaM] р + k[(Tp+ \)kp + к] Следовательно, после подстановкир =7(0 получим

q(a)-

q{a)

= 0.

Х=кМ<)-[Т,-TJ,iaq(a) + llq2(a) + k,kMa)]i£, =0,

\-T qXa)(i)+k\kQq{a)-kk

TXq,{a)-k,k,l\i

(о-*=0.

Для исследования влияния параметра на собственные колебания да1И10Й системы вырази.м величину к из каждого уравнения по отдельности;

(7(G)

Jtq{a)

kq{a)

.k,q{a)

(18.97)

[ q\a) k,qXa)

k,qXa)

(18.98)

. Задаваясь разными значениями a = (2 , для каждого из них по .этим уравнениям строим две кривые к (о)) (рис. 18.19, б). Точка их пересечения дает соответствую-П1ие значения u) и . В результате можно построить графики (рис. 18.19, виг) зависимостей амплитуды а и частоты ю периодического решения от параметра к (каждое поспроение па рис. 18.19, б дает по одной точке на каждом из rpacJjiiKOB рис. 18.19, (З и г).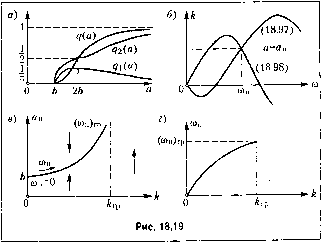