Передаточная функция звена kp

(4.52)

=) с

x, = щ R

Х2 - U2

Х2 = Щ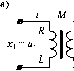

1 + Тр

Звено условно можно представить в виде двух включенных последовательно звеньев - идеального дифферепцируюн1его и апериодического первого порядка.

Парис. 4.21 изображены примеры диффсренцируюпшх звеньев с за.медлснием. Наиболее часто употребляются электрические

цепи (рис. 4.21, а, б и в). В ггекоторых случаях используются дифференцирующие устройства, состоящие из гидравлического демпфера и пружины (рис. 4.21, г).

Составим, например, уравнение для дифференцирующего конденсатора (рис. 4.21, а). Ток в рассматриваемой цепи определяется уравнением

Рис. 4.21

idt = м.

Переходя к изображепия.м и решая это уравнение относительно тока, получаехк

t/,(P) рс

1(р) =

ihip)-

Напряжение на выходе цепи

U2{p) = RI(p) =

Тр \ + Гр

где Т= RC - постоянная времени цепи.

Времеп1И)1е характеристики звена приведет)! в табл. 4.6, а частоттле - в табл. 4.7.

Амплитудно-частотная характеристика имеет иной вид, чем у идеального звеиа. Характеристики совпадают в области низких частот. В области высоких частот реальное звено пропускает сигнал хуже, чем идеальное звено. Коэффициент передачи стремится к значению /7 при oi-oo, Ддя звеньев, представляющих собой RC- или RL-iimb (рис. 4.21, а и б), k = Ти на высоких частотах коэффициент передачи стремится к единице.

Фазовые сдвиги, вносимые звеном, являются наибо;И)ШИМи при низких частотах. На высоких частотах фазовый сдвиг nocTeneinio уменьншется, стремясь в пределе к пулю при (о оо. Здесь также видно, что это звено ведет себя нодобпо идеальному только в области низких частот.

Л. а. x. строится по выражению

L(co) = 201g , . (4..53)

82 Непрерывные линейные системы автоматического управления

Асимптотическая л. а. х. может быть представлена в виде двух прямых. Одна и.з них имеет положительный наклон 20 дБ/дек (при со < i/O, а вторая - параллельна оси частот (при со > 1/7).

§ 4.8. Неустойчивые и минимально-фазовые звенья

Рассмотренные выше звенья позициоиносо тина относятся к устойчивым звеньям, или к звенья.м с самовыравниванием. Под са.мовыравнивание.м пони.мается способность звена самопроизвольно приходить к новому устагювивше.муся состоянию при ограниченном изменении входной величины или возмущающего во.здействия. Термин самовыравниванив обычно при.меняется для звеньев, представляющих собой объекты управления.

Существуют звенья, у которых ограниченное изменение входной величины или возмущающего воздействия не вызывает прихода звена к иово.му установившемуся состоянию, а выходная величина имеет тенденцию неограниченного возрастания во времени. К таким звеньям относятся, например, звенья интегрирующего тина. Они были рассмотрены вьш1е.

Существуют звенья, у которых .этот процесс выражен еще заметнее. Это объясняется наличием положительных вещественных корней или ко.мнлекспых корней с положительной веществешюй частью в характеристическо.м уравнении, в резу;1ьта-те чего звено будет относиться к категории неустойчивых звеньев. Вопрос устойчивости будет изложен подробно в главе 6. Рассмотри.м в качестве примера звено, описываемое дифференциальным уравнением

Tdx.2/dt-Х2 = kx , (4.54)

которому соответствует передаточная функция

W(p) =

-1 + Гр

(4.55)

Переходная функция такого звена представляет собой показательную функцию с положительным показателем степени:

/г(0 = Ке1) 1(0 (4.56)

Эта функция изображена на рис. 4.22.

Таким звеном может быть, например, двигатель любого типа (рис. 4.10, а) если его механическая характеристика, т. е. зависимость в1)ащающего момента от скорости вращения М =/(), имеет положительный наклон. На рис. 4.23 изображены разновидности механических характеристик двигателя. В случае, соответствующем кривой 1, двигатель представляет собой устойчивое апериодическое звено первого порядка, уравнения движения KOTojjoro были рассмотреть в § 4.5. Это звено имеет гюложительное самовыравнивание.

В случае, соответствующем кривой 2, когда вращающий момент ие .зависит от скорости враи1еиия, уравнение движения двигателя, заниса1июе для уг.товой скорости, приобретает вид

J- = k.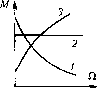

Рис. 4.23

где/ - сум.марный приведеи/гый момст инерции двигателя, k - коэффициент пропорциональности между управляющи.м воздействием х, и вращакнцнм моменто.м. Здесь скорость двигателя связана с управляюнгим воздействием передаточной функцией, соответствующей интегрирующему звену

jp р

Это звено не имеет самовыравнивания. В случае, соответствующем кривой 3, ди()-ференциальное уравнение движения будет

где - naicTOH механической характеристики в точке, где производится линеаризация. Это уравнение приводится к следуюн1е.му виду:

где Т =УД, - постоянная времени двигателя.

Уравнение совпадает с выражением (4.54). Звено и.меет отрицательное са.мовы-равпивание.

Признако.м отрицательного самовырав1ИП!ания является отрицательный знак перед самой выходной величиной в левой части дифференциального уравнения (см., например, формулу (4.54)) или появление отрицательного знака у с1К)бодного члена знаменателя передаточной функции (см., например, фор.мулу (4.55)).

Существенной особенностью неустойчивых звеньев является наличие б6льиН1Х по сравнению с устойчивыми звепья.ми фазовых сдвигов. Так, для рассматриваемого апериодического звена с отрицателыгы.м са.мовыравнивапие.м (неустойчивого) частотная передаточная функция па основании (4.55) будет равна

Щ;(0) =

(4.57)

Модуль ее не отличается от модуля частотной передаточной функции устойчивого апериодического звеиа (табл. 4.3):

Л((0) =