x{t) = g{t) - y{t) (5.3)

- ошибка системы.

Для получения дифференциального уравнения всей системы уравнения (5.1) - (5.3) решаются относительно ее Bbixoimoft величитп)!, в качестве которой можно рассматривать как управляемую величину y{L), так и ошибку x{t).

В первом случае получается дифференциальное уравнение

D{p) y{t) = В{р) g{t) + N{p)Kt), (5.4)

Dip) = Bip) + dp); B(p) = B,(p) B(p);

Cip) = Co(p) C,(/;); N(p) = C/p) N,{p).

Полино.м D{p) n-ro порядка характеризует свободное движение системы автоматического управления. Он называется характеристическим полиномом замкнутой сист.емы и может быть представлен в виде

D(p)-aop + a,p + +а ,р + а , (5.5)

где .....я в линеаризованной систе.ме представляют собой постоянные коэффициенты.

Как видно из (5.4), полино.м D(j)) отличается от характе1)истического полино.ма объекта Cq(p). Это означает, что и свободное движение систе.мы .может cyntecTBeniio отличаться от свободного движения объекта. В частности, если управляемый объект неустойчив, то при правильно выбранных алгоритме управления и параметрах управляющего устройства система в целом будет устойчивой. Наоборот, при неправильном выборе систе.ма авто.матического управления устойчивым объектом может стать неустойчивой.

Полином В{р) в уравнении (5.4) определяет в;1ияние задающего воздействияg(r) иа характер изменения управляемой величины у(1), причем последняя должна как можно более точно воспроизводить задающее воздействие, т. е. ошибка систем ы (5.3) должна быть .мипи.малыюй.

Полином N(j)) определяет влияние возмущаюп1его воздействия /(С) иа ха1)актер изменения управляемой величины y(L). В уравнении (5.4) учтено только одно воз--мущеине f(t). В принципе таких возмущений может быть несколько. Однако вследствие линейности уравнения действует принцип суперпозиции, согласно которому реакция па сум.му воздействий равна сумме реакций. Поэто.му достаточно рассмотреть методику учета только одного возмущения, а при наличии нескольких возмущений необходи.мо лишь просуммировать результат.

Во втором случае, когда в качестве выходной величины рассматривается ошибка х(г), дифференциальное уравнение системы .может быть получено нодста1ц)вкой в (5.4) выражения для ошибки (5.3):

Dip) x(t) = С{р) g(t) - N{p) fit). (5.6)

Из (5.6) вытекает, что ошибка системы автоматического управления может быть представлена в виде суммы двух составляющих. Первая составляющая определяет-

88 Непрерывные линейные системы автоматического управления

ся наличием aa/iaioniero иоздейстиия g{t), а вторая - наличием возмущающего воздействия (в общем случае - возмущаюнщх воздействий). Первая составляющая не равна нулю только в ирограм.мных и следяhuix системах. В стабилизируюн1.их системах g{t) = const. Поэтому всегда можно выбрать начало отсчета так, чтобы g{t) = 0.

Согласно (5.4) N{p) = С(р) {р). Это означает, что выбором структуры и иара-.метров управляющего устройства можно у.меньшить вторую составляющую ошибки и тем самым ослабить влияние воз.мущающего воздействия на об1>ект. Если для какого-либо возмущающего воздействия полином N{p) = О, то говорят, что система автоматического управления является инвариагггпой относительно этого воздействия. Равным образом в нрогра.м.мгнлх и следянп1х системах равенство С{р) = О означает, что система инвариантна относительно задающего во.здействия.

Уравнения (5.1), (5.4) и (5.6) могут быть также представлены в виде совокупности уравнений первого порядка, называемых уравнениями состояния. Они рассматриваются в § 5.5.

§ 5.2. Передаточные функции систем автоматического управления

Записанные выше дифференциальные уравнения системы автоматического управления (5.4) и (5.6) могут быть получены также на основании понятия передаточной 4)упкпии, которое было введено в главе 3. Рассмотри.м рис. 5.1, где изображена замкнутая система авто.матнческого управления.

Предположим вначале, что чувствитечьный элемент (ЧЭ) отсоединен от управляемого объекта (УО), и рассмотри.м так называемую разомкнутую систему автоматического управления.

Управляющее воздействие, которое прикладывается к унравляемо.му объекту, определяется выражением

u{t)=W{p)x{t), (5.7)

гдех - рассогласование па выходе чувствительного элемента, WyQj) - передаточная функция управляющего устройства, которая определяется из дифференциального уравнения управляющего устройства (5.2):

щр) =

Ujp) Мр) х(р) с,(рУ

(5.8)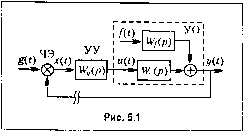

Управляемая величина может быть найдена из выражения

y{0 = Wo(p)u(t) + Wf(p)m, (5.9)

где Wo(j)) - передаточная функция об1>ек-та но управляющему воздействию, Wj(j)) - передаточная функция объекта по воз.му-щающему воздействию f(t).

Первая из них определяется из дифференциального уравнения объекта (5.1) при fit) = 0:

а вторая - из того же уравнения при м(0 = 0:

Fip) C,ip) (--ll)

Подставляя (5.7) в (5.9), получаем

yiL)-Wip)xii) + \Vj{p)Jit). (5.12)

Здесь введена так называемая передаточная функция разомкнутой системы

N пгг чпл. ч о(Р)ВЛр) Bip) U(.) = U.(pK(P> = -. (5лз,

Передаточную функцию разомкнутой системы можно определить как oTiioine-ние изображе1И-1Й управляемой величины и ошибки при пулевых началыи)1х значе-}1иях и возмущаюнигх воздействиях, равщях ггулю:

гдер = с +7(0 - комплексная величина.

При.менительно к функциям BpcMeini, которые использовались в формулах (5.7), (5.9) и (5.12), передаточная фу1п<ция разомкнутой системы дает воз.мож1гость в символической или операторной фор.\1е записать дифференциальное уравнение, связы-ваюп1ее управляемую величину yit) с огнибкой ,г() в разомкнутой системе:

yit) = Wip) xit), (.5.15)

гдер = d/dt - оператор дифферепцирования.

Учитывая (5.13), фор.мулу (5.15) можно также за1И1сать в виде

Cip)yit) = Bip)xil). (5.16)

Передаточная фун<ция разомкнутой системы имеет весь.ма большое значение в теории автоматического управления, так как многие методы апа.,1иза и синтеза основаны на использовании именно этой функции.

Рассмотрим теперь замкнутую систему, т. е. предиоложи.м, что чувствительный элемент соединен с объектом. При этом можно использовать так называемое уравнение замыкания (5.3):

xit)-git)-y(t). (5.17)

Решая (5.12) и (5.17) сов.местно, получаем для управляемой величины