§4.5. Позиционные звенья

Характеристики позиционных звеньев сведены в табл. 4.2 и 4.3, 1. Безынерционное звено. Это звено не только в статике, но и в дина.мике описывается алгеб1)аическим у[)авнепием

Перед&точпая функция звена равна постоянной величине:

(4.20)

(4.21)

Примеро.м такого звена являются механический редуктор (без учета явлегшя скручивания и лк)()та), безынерционной (ншрокополосный) усилитель, делитель иа-иряжешя и т. п. Многие датчики сигначов, как, например, потенциометрические датчики, индукционные датчики, вращающиеся транссорматоры и т. п., также могут рассматриваться как безыперциоиные звенья.

Переходная функция такого звена представляет собой ступенчатую функцию (табл. 4.2), т. е. [фи х,(/) = \{t), X2{t) = h{t) = k- Функция веса представляет собой импульсную функцию, площадь которой равна к,т.е. прих(0 = 5(:2(0 = w{t) = = k8(t).

А. ф. x. вырождается в точку, расположенную на вещественной оси на расстоянии к от начала координат (табл. 4.3). Модуль частотной передаточной функгщи /1((о) = к постоянен на всех частотах, а фа;ювые сдвиги равны пулю (ц1 = 0),

Безынерционное звено является некоторой идеализацией реальных звеньев. В действите.чьности пи одно звено пе в состоянии равпо.мерно пропускать все частоты от о до оо. Обычно к такому виду звена сводится одно из реальных звеньев, рас-с,мат1)иваемых ниже, например апериодическое или колебательное, если .можно пренебречь влиянием динамических (переходных) процессов в этом звене,

2. Апериодическое звено первого порядка. Звено описывается дифференци-а.чьны.м уравнением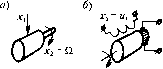

£2 = const

X2=t

Х,-и R

T + :,.=kx,. (4.22) dt

Передаточная функция зве1[а

W(p)-. (4.23) i + Tp

Примеры а[1ериоднчес-ких звеньев первого порядка изображены на 1)ис. 4.10.

В качестве первого примера (рис. 4.10, а) рассмат-

ривается двигатель любого Tinia (элект])ический, гидравлический, пневматический и т. д.), механические характеристики которого (зависимость в])ан1аю1цего MOMeirra от скорости) могут быть представлены в виде параллельных прямых (рис. 4.11). Входной величиной X, здесь является уиравляю[пее воздействие в двигателе, напри.мер подводимое напряжение в ;олектрическох[ двигателе, расход жидкости в гидравли-ческо.м двитате.че и т. п. Выходной величиной является ско])ость врапкмшя Q. /1иф-ференциальное уравнение движения при равенстве пулю .момента нагрузки Л[ожет быть представлено в виде

dt. iin

vjiej- приведенный к валу двигателя суммарный момент пперпии; ky, -- коэффициент пропоргиюиальпости между управляющи.м воздействием х, и вращающи.м моме1ГГО.м; к, = М,)/Оо - иак-тои механической .характеристики, равный отношению пускового мо.\[ента к скорости холостого хода при иекоторо.м значении управляющего во.здействия.

Это уравнение приводится к виду

Т-+ Q = кх

где к = мД) -- коэф(})йциепт передачи звена, 7 = J = J- - постояттая времени

Мц к,

двигателя. Оно полностью совпадает с (4.22).

В качестве второго нри.мера (рис. 4.10, б) приведен электрический генератор постоянного тока, входной величиной которого является напряжение, подводимое к обмотке возбуждения м а выходной - напряжение якоря

Апериодическими звеньями первого порядка являются также резервуар с газо.м (рис. 4.10, в), у которого входная величн[[а представляет собой давление перед впускпы.м отверстие.м, а выходная - давленnepj в резервуаре, и нагревательная печь (рис. 4.10, г), у которой входная величина - количество поступающего в единицу вре\[е[и тепла Q, а выходная - температура в печи /ц.

Электрические RC- и ЬЯ-цепп в соответствии со схе.ма.ми, изображепны.ми па рис. 4.10, д, также представляют собой а[[ериодические звенья первого порядка.

Во всех приведенных примерах дифферсЕЩналь-ное уравнение движения совг[адает с (4.22).

Г1ереход[ая функция Г[редставляет собой эилю-пепту (табл. 4.2). Миожт[тель l(t) указывает, что экспонента рассматривается, начиная с мо.меита t О,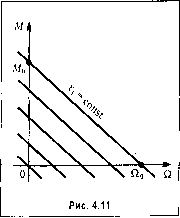

Таблица 4.2. Временные характеристики позиционных звеньев

тип звена и его передаточная функция

переходная функция

функция веса K)(t)

Бсзыперциоипое W(p) = k .

h{t) - k т

оГ t w{t) = kh{t)

Апериодическое 1-го

порядка

W(j))=k/].+Tp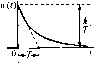

h{t) = k

1-е

Апериодическое 2-го порядка

M]p + Tip

(1 + ГзР)(1 + Гзр)

2 V 4 {Т,>2Т;Т>Т,)

h(t) .Т+Т,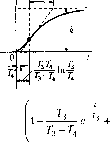

e 3 -e

1(0

h(t) = k

-1(0

Колебательное

2 2

\ + 21,Гр+Г-р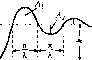

uit)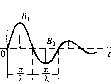

7=-lii-;

1t l>2

h(t)=k

r- 1

3- -----

l-e 1(0

cosXt +

ш(0 = -e-sinXfl(0