нужно в соответствуюпше передаточные функции иодставитьр = +;со, что дает

а =-

г, (3 = arctg

Г, (О

(анатогичные выражения получаются для а \1у). СраВ1И-1вая ихс (18.149), приходим к выводу, что в формулах (18.151) и (18.152) вместо а, Та>, аа>, Гз ) должны быть поставлены соответственно выражения;

а 7] (О асо 7 2 со

ТТтс ТТт uJ ТТт

(20.50)

В результате q и q будут функциями всех трех величии: q {а, со, Q; q (а, со, Q, Характеристическое уравнение в.место (18.155) примет вид

Ьор + 6,+Ь2р- + р + kiip- О + 9(а,ш,О = О,

После подстановкир = С по формуле (20.19) нолучае.м веп1ествс1Н1ую и мнимую части:

X = kq {а, (О, О + 6iC боС бзС + С - (бАоС + 36iC + 2б2)со + = 0; Y-kq (а, ю, О + (46oi; + 36,!; + 2/;2С + 1 )ю - {АЬ<, + 66,)ю- = 0.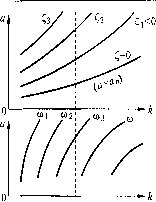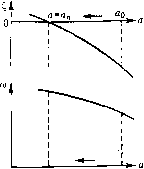

Отсюда находим:

(a,co,0=/i(M,0, <7(а.м,О=/2((0,О. (20.51)

Будем задаваться разными зиачения.ми и со и строить на основании уравне1И1Й (20.51) .типии равных значений и со на плоскости координат k, а (рис. 20.14). Для этого для заданных , со сначала строится кривая о-тоикшя q {а)/q (а) (рис. 20.15). Согласно (20.51) это отношение должно быть равно определенному числу: q {a)/q (а) = = /1 2, чем определится значение а (рис. 20.15) для данных , со. После этого для них вычисляется значение k fi/q. Таким путем поточка.м строится вся диаграм.ма качества нелинейного переходного процесса (рис. 20.14). Линия = О соответствует зависимости амплитуды установившихся автоколебаний от коэффициента усиле1и-1Я k.

При любом заданно.м k изменение показателя затухания С, и из.менение частоты со во время переходного процесса определится пря.мой k = con.st (рис. 20.14, пунктир). Результат показан па рис, 20.16. Это позволяет судить о быстроте ;iaтухаиия и о количестве колебаний .за время переходного процесса.

Заметим, что решение задачи несколько упростится при малом С- В этом случае, считая постоянные времет! из,мерителей и Г2 достаточно малыми, .можем иреиеб-[)ечьпроизведепиями ТСи Т2С,в выражениях (20.50) и пользоваться прежними выра-же1тями q и с/ (18.151) с подстановками (18.151) и (18.152). Кроме того, в написап-пых выше выражениях для X и У нужно сохранить только первую степень I;.

X = kq{a,(i,) + C,- (З61С + 2h2W + о = 0; У = kq (а, (О) + (2Й2С + 1)со - {АЬС, + 6/)i)co- = 0.

В принципе решение не меняется. Изложенный метод решения задачи отличается тем, что он одинаково пригоден к ра.зличиы.м системам, описывае.мы.м уравиепияхт любого порядка, и пе связан с построением годографов па комплексной плоскости.

Более подробно применение логических устройств, нелинейных атгорит.мов управления и пелинейных корректирующих средств рассмотрено в работах [74,75,941 и др.

Глава 21

ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ

§ 21.1. Симметричные одночастотные вынужденные колебания

Проблема анализа вынужде1Н1Ых колебаний нелинейных систем вообп[е является весь.ма сложной и многообразной. Поскольку принцип наложения решений (суперпозиция) здесь неприменим, то, вообще говоря, нельзя складывать частные ренюния ири различных В1ЮШПИХ во;!действиях, найденных по отдельности, а также складывать свободные и вынужденные колеба1Н1Я. Особое нелпнейпое сложение решений во:!.М()жио в случае, если реиюния разделяются но степени медленности протекания их во времени

(т. е. по значению возможных частот колебаний), аналогично тому, как эта делалось в главе 19. При этом каждое из складывае.мых ренгений существенно зависело от другого, а и.менно а.мплитуда автоколебаний супюственно зависела от величины смещения, характеризующей медленно протекающие процессы. Такого же рода разделение penie-ний для вынужденных колебаний будет рассмотрено ниже, где появится воз.можность рассмотрения нелинеЙ1иях двухчастотиых колебаний с большой разностью частот.

Не касаясь сложных фор.м вынужден1н>1х колебаний нелинейных систем (хотя их исследование также имеет больнюе практическое значение), ограничимся в данном параграфе определением одночастотных вынужденных колебаний, когда колебания систе.мы происходят с частотой внепи1его периодического во.здействия. Форма колебаний, как и прежде, па основании свойства фильтра будет считаться близкой к синусоидальной для переменной х, стоящей под знаком нелинейной функции. При рассмотрении вынужденных колебаний во многих случаях возникают ограничения, накладываемые на амплитуду и частоту внешнего периодического воздействия (зависящие также и от параметров системы) и обусловливающие существование одночастотных вынужден1И)1Х колебаний в нелинейной систе.ме. Будем их кратко называть условиями захватывания (в указанном пнц)оком смысле). Особое значение эти условия приобретают для автоколебательных систем при частотах, близких к частоте автоколебаний и вьипе.

Итак, пусть имеется некоторая нелинейная автоматическая система, в любо.м месте которой приложено виенпгее синусоидальное воздействие

/(О = В sin (О/. (21.1)

Пусть уравнение дина.мики системы приведено к виду

Q{l>)x + Rip)F (.г, px) = Sip)f{t) (21.2)

Выполнение условий фильтра (§ 18.2), а также выводимых ниже условий захватывания (где это необходи.мо) позволяет в нервом приближении искать решение для установившихся вьпгужденных колебаний систе.мы в cииycoидaиJHoй форме

X = а sin (со/-t-ф), (21..3)

где искомыми неизвестными постояипы.ми будут амплитуда а и сдвиг фазы ф, в то время как частота (0 здесь уже задана выражением (21.1). В отличие от такой типичной постановки задачи можно будет, конечно, в да-тьнейше.м решать и обратную задачу определения потребной частоты со или амплитуды В внешнего во.здействия ио заданной амплитуде вынужденных колебаний а и т. п.

Чтобы иметь воз.можность применить тот же общий подход к решению задачи, который был принят при отыскании автоколебаний, выразим в уравнении (21.2) переменную /черезх. Согласно (21.1)

/(i) = В sin [(со/ -I- ф) - ф] = В cos ф sin (со,/ -t- ф) - В sin ф cos (cot -t- ф).

Отсюда, принимая во внимание выражение (21.3) для х и выражение для его производной

рх = а со cos ((й,/-ьф).