Полученные выражения для матриц передаточных функций замкнутой системы позволяют использовать формулы, аналогичные формулам § 5.2, но записанные уже для матриц-столбцов ошибок и управляемых величин. Так, например, для матрицы изображений ошибок имеем

Х{р) =

Х2(Р)

= Ф,(р)С(р)-Ф(р)Р(р).

(5.120)

Исходные дифференциальные уравнения м]10гомерной системы могут быть также представлены в виде уравнений состояния:

х = Ах + Ви+ Mf; у=Сх;

(5.121)

В этих выражениях х = [х х2.....x f - матрица-столбец переменных состояния,

п - порядок дифференциального уравнения.

Характеристическое уравнение, соответствующее системе (5.121), имеет вид

Ep-A-BD =0,

(5.122)

где Е - единичная матрица пхп.

Выбор переменных состояния для многомерных систем (в отличие от одномерных) представляет собой сложную задачу и здесь не рассматривается.

Условием полной управляемости многомерной системы является невырожденность матрицы Калмана

В, АВ, АВ,...[а) В а условием полной наблюдаемости - невырождетюсть матрицы

C\Ac\(¥fc\...(A) ~c

(5.123)

(5.124)

Матрицы (5.93) и (5.99) представляют собой частные случаи матриц (5.123) и (5.124).

Глава 6

КРИТЕРИИ УСТОЙЧИВОСТИ

§6.1. Общие сведения об устойчивости

Устойчивость является одним из главных требований, предъявляемых к автоматическим системам.

Для иллюстрации понятия устойчивости обыч1ю приводится следуюпитй пример (рис. 6.1). Состояние равновесия тара в точке на рис. 6.1, а устойчиво, так как если какие-либо вне1пиие силы выведут тар из этого состояния (например, в точку А, или Лз), то он возвратится к точке А. Состояние равновесия в точке А па рис. 6.1, а неустойчиво.

В этом примере, как и в теории устойчивости, полагается, что впепнтие силы или возмущения прекращают свое действие к некоторому моменту времени, который можно принять за начальный момент = 0. Такие возмущения часто называют исчезающими.

Применительно к системам автоматического управления такое понятие устойчивости можно использовать лишь частично для характе]5истики свойств их объектов, которые сами по себе .могут быть устойчивы.ми или неустойчивыми. К пОсле-днихМ относятся, например, некоторые ракеты.

Автоматические системы отличаются тем, что в них, во-иервых, осуП1ествляется специально оргайизоваппое управление объектом. Благодаря ему система с неустой-чивы.м объектом может стать устойчивой, а система с устойчивы.м объектом (при неправильном управлении) - иеусгойчивой. Так, неустойчивое состояние равновесия шара на рис. 6.1, б легкими прикосновениями можно сделать устойчивы.м, а шар на рис. 6.1, а те.м же способом можно раскачать так, что амплитуда колебаний будет увеличиваться.

Во-вторых, при наличии исчезающих задающего и возмушаюпшх воздействий система .может иметь много состояний равновесия. Так, систе.ма стабилизации напряжения в электрической сети при номинально.м токе нагру.зки (возмущающем воздействии) поддерживает заданное значение напряжения, а при увеличении тока нагрузки из-за подключения донолнительпых потребителей переходит в другое состояние равновесия, отличающееся пониженным значением напряжения.

В-третьих, для ряда систем типичным режимом работы является движение. Так, исполнительная ось следян1ей системы в процессе слежения движется с ]юстоя1П1ой или переменной угловой скоростью, закон из.менеиия которой в общем случае может быть случайным. Состояние равновесия можно рассматривать как простейпшй частный случай движения.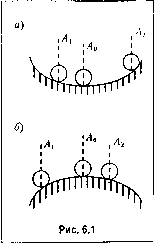

В классической теории устойчивости исследуется ]ie устойчивость систе.мы как таковой, а устойчивость ее так пазывасмого невозмущенного движения.

Ниже будет иока;5апо, что для линейных систем с точки зрения устойчивости не имеет значения, какое их движение п])инимается в качестве невозмущенного. Это можетбыть, например,состоя]те равновесия системы стабилизации напряжения при любом (даже не заданном)-токе нагрузки или движение исполнительной оси следящей сис те.мы по случайному закону. Однако для нелинейных систем это имеет существенное значе]1ие, так как одно конкретно заданное невозмущенное движение может оказаться устойчивым, а другое - неустойчнвы.м.

Исчезнувнше к моменту времени f = О возмущения вызывают отклонение двн-жегшя системы от ее невоз.мущенно1о движенргя. Это новое движение называется возмущенньш.

Строгая математическая теория устойчивости была создана Л. И. Лянуновы.м и изложена и.м в ])аботе Общая задача об устойчивости движения , опубликованной в 1892 г. В ней было определено понятие устойчивости и разработаны методы устойчивости нелинейных систем.

Отправные ноложення,Tia которых базируется понятие устойчивости по Ляпунову, рассмотри.м на примере систе\п>1 второго порядка. Для характеристики движения этой системы исиользуемнере.менные состояния (см. гл. 5)Xi их2. На плоскости (рис. 6.2) они определяют положение некоторой точки М. В процессе движения системы X, II л2 из.мепяются, а точка М прочерчивает некоторую траекторию.

Положи.м,что невозмущенному движению соответствует траектория 1, на которой x(t) = x(t), Х2(!:) = .12(0 Начальными значениями для нее будут xf (0) = xfo, Х2(0) = Х2о (точка Mq ). Пусть исчезнувшие к мо.менту времени с = О возмущения изменили начальное состояние систе.мы и пачальиы.мизпачения.ми сталих5(0),Х2.(0), которым соответствует точка Mq. В результате движение стало воз.мущеппым (кри-

вые 2 или 3). Отклонения начальных значеннн обозначим Дхю = х,(0)-х]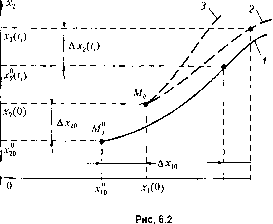

А-,(г,)