Система с пере.мениой структурой. Как уже ука.зывалось в главе 2 системы с перемеииой структурой! содержат в себе специальное переключающее устройство для нз.мепе1Н[я у((рав-ляющего устройства, которое срабатывает в зависи.мости от размеров и знаков входных величин.

При.мер иереключаюптего устройства приведен схематически па рис. 16.27, где КЭ - ключевой элемент, БИС - блок изменеиня структуры. Его уравпепис [32] принято за[1исывать в виде

i-----

-*{бис

Рис. 16.27

и = Ц1Х.

(16.70)

Функция \/ может строиться по-разно.му Например,

а при .r,x>0, Р при .rj.r<0.

(16.71)

Основная характерная нелинейность .здесь состоит в самом факте автоматически го переключения в зависимости от состояния входных величи[т

Глава 17

ТОЧНЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ

§ 17.1. Фазовые траектории

и метод точечных преобразований

Понятие о фа.зово.м пространстве, о фазовых траекториях и их типах было уже дано вьнпе. В данном параграфе па примерах построения фазовых траекторий для простейших систем второго порядка будут проиллюстрированы некоторые важные особенности процессов в нелинейных системах автоматического управления.

П р и .м е р 1. Возь.мем cncre.vfy авто.матического управления с объектом без са-мовыравпивапия и с приводом управляющего органа, имеющи.м постоянную скорость. Уравнение объекта будег

7 РФ =

(17.1)

Для управляюпдего устройства без массы и демпфера с жесткой обратной связью, т. е. при 5г1 = -ф, а = л - С, С получим

1 S

(17.2)

где ф, г], , С и а - относительные изменения управляе.мой величины, смещений чувствительного элемента, управляюп1его органа, элемента обратной связи и управляющего золотника (рис. 10.11, а), 6 - коэффициент.

Пусть привод управляющего органа и.меет постоянную скорость в двух вариа]1тах; 1) с мгновенным переключением (рис. 16.22, ж) при переходе управляющего элемента (золотника, струйной трубки) через нейтральное положение (о = 0); 2) с зоной нечувствительности (рис. 16.22, з) вследствие наличия перекрытия золотника или струйной трубки. В первом случае уравпение привода управляющего органа будет

р = с sign о.

а во втором

= О при \ а\<Ь,

p = csigna прна>й.

Возьмем фазовую плоскость (х,у), притшв

х=ф, ,г/=рф.

Из уравнений (17.1), (17.2) и (17.5) имеем

(17.3)

(17.4)

(17.5)

(17.6)

Следовательно, переключения привода в нервом варианте (о = 0) будут иметь место при

х=-ЪТ у, (17.7)

что соответствует прямой АВ (рис. 17.1, а) па фазовой плоскости, причем согласно (17.6) значениям а > О соответствует часть плоскости слева от прямой АВ, а о < О - стфава.

На осповапии первого из соотношений (17.6) с учетом (17.3) прн а< О получаем

dy с

а из (17.5)

(17.8)

откуда находим уравнения фазовых траекторий

dy с

dx Т у

(17.10)

или, после интегрирования.

Это есть семейство парабол, показанное па рис, 17.1, а справа от линии АВ (они си.мметричны относительно оси х). Так как (17.8) и (17,9) являются проекния.ми скорости V изображающей точки М на оси х и у, то имеем Vy < О, а знак 1)д. совпадает со знаком г/. В соответствии с этим па рис. 17.1, укажем стрелочками направление движения изображаюп1ей точки М по фа.зовым траекториям. Аналогичным путе.м легко строятся параболы слева от прямой АВ.

В результате, как видно из обпюго расположения фазовых траекторий (рис. 17,1, а), получается устойчивая система с затухающи.м колебательным переходным процессом. Но чисю колебаний будет конечны.м. В самом деле, здесь и.меется особый отрезок CD, в который вливаются все фазовые траектории. Чтобы выявить поведение систе.мы на этом отрезке, вспомним, что для него сог.тасно (17,7) и (17.5)

57 ф - ф = О, или ф = Сое

Следовательно, попав на отрезок CD, изображающая точка ие можете пего уйти, и система будет апериодически приближаться к установившемуся состоянию, т. t. изображающая точка будет сползать по отрезку CD к началу координат О. Таким обра.зом, имевший .место вначале колебательный переходный процесс после конечного числа колебаний вырождается в этот так называемый скользящий процесс.

Р<Р 1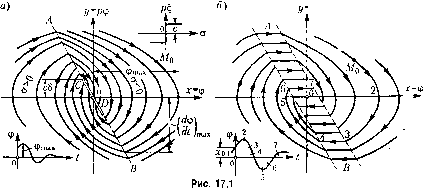