Решение уравнения (21.24) будем искать в виде

х = х + х*, лг* = а .sin (ш £ + ф), (21.26)

где х° - медленно .меняющаяся составляющая, а х* - колебательная составляю1ная, а.мплитуда а и фаза ф которой в общем случае тоже медлеппо изменяются во времени.

Тогда гармоническая линеаризапия нелинейности ¥{х, рх) может производиться но фор.муле, аналогичной (19.5):

F(x,px) = F +qx* +-3-рх*,

(21.27)

f = f x + a sim/, со cos\/</v/; 1

q=- (x +a sinv, a,a} cosv;)sinv;(iv;;

tt/7 \

f{x + a sin v/, a,(0, cosV(/1cos

0 2n

(21.28)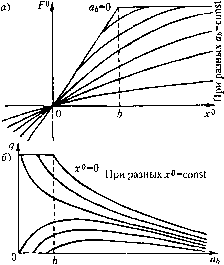

приче.м Ц1 = ф,/, + ф. Из сравнения этих фор.мул с (19.6) видно, что при отыскании вынужденных колебаний .можно целиком пользоваться все.ми конкретными выражениями для F, q и q, приведенными в главе 19. Таким образо.м, для каждой конкретной нелинейности имеются готовые выражения:

f (х а а) ), q (х . а, ш ), q (х а ш,).

(21.29)

причем часто величина со в них отсутствует. В качестве примера на рис. 21.6 приведены эти зависи.мости для ггелинейности типа насыщения, аналогичные приведенным в главе 19.

По анааогии с формулой (21.4) запишем

.sinф

COSф--р

Подставив выражения для/ (л-.рлг),/2 (О и л: в заданное дифференциальное уравнение нелинейной системы (21.24), нолучим уравнение

Q{p){x+x*) + R{p)

+qx*+-px*

= 5,(р)/,(0 + 52(р)-

С08ф--- р

которое разбивается нелинейным образом (см. главу 19) на два уравнения соответственно /1ЛЯ медленно меняющихся и для колебательных составляющих:

Q{p)x+R(p)h-S,(p)f,(ty, (21.31)

Q(p)+S2iP)-

.Slnф С05ф---р

х* = 0.

(21.32)

Оба уравнения содержат все три неизвестные а, ф и х .

Второе из ;)тих уравнений совпадает с прежним уравнением (21..5), но только с игн>[мп коэс{}фициента,мн гармонической линеаризации q и с/, зависящими от величины смешения х . По;)тому уравнение (21.32) до конца решается только совместно с уравнением (21.31), хотя, как будет видно из дальнейшего, возможны и более простые случаи. Пока же можно, написав характеристическое уравнение вида (21.12), после подстановки р =jiu привести уравпегше (21.32) к следующему:

(21.33)

в результате решения которого любым из двух методов (графическим или аналитически.м), описанных в § 21.1, определяются зависимости амплитуды a и сдвига фазы Ф от величины смещения.х°, т. е.

(21..34)

ав(х%, В), ф(х°,со ,В),

гдех остается пока enie иеизвестиым.

Для нримецепия графического метода §21.1 к отысканию зависимости а (х ) по уравнению (21.33) нужно иарис. 21.1 построить серию кривых 7(ав) для разных значений х° = con.st, которые согласно (21.28) входят в выражения для q и q. Уравнение аналитического метода (21.17) примет вид

X(coJ + F(co )

X(co ,fl x ) + y(co, a ,x )

(21.35)

гдеХ2, У2 и X, У обозначают вещественные и мни.мые части соответственно для выражения 52 ОЮв) и выражения

Q Осо ) + R OcoJ [q (а, со , х ) +jq (а w , x°)J.

Уравпение (21.35) не решается так просто, как (21.17). Однако можно нри.мен1ггь следующий графический прием его рсчпення. Ра.збив (21.35) на два уравиепия;

Х((0 ) + У22((0,.)

Х2((й а ,.г°) + у2((й ,а,...г- )

построим по первому и;з них на плоскости (, я ) кривую 1 (рис. 21.7), а по второму -серию кривых2 для разных значений.г* = const при :)адапных б им. Перенося полученные точки пересечения кривых вп[)аво на плоскость.а, получаем сразу искомую зависимость {х) для заданного внешнего периодического воздействия, т. е. для заданной пары значений В и ш . Эту зависи.мость легко получить таки.м же путем и д.тя любых других заданных В и ш .

Подставив теперь значение амплитуды а в первое из выражений (21.29), найдем

функцию смещения в виде

B-con.st (oe=const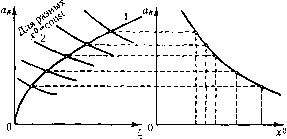

Рис. 21.7

а) f0=O(i-0)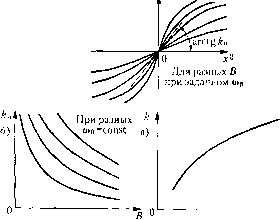

При .заданных юв и В

7- = cD(.r°,co ,/i), (21.36)

которая является характеристикой данного пелинейного звена системы поотпопюггию к.медленно меняюпп1мся соста15Ляющнм пе[)смен1гых /-и.г. Эти медлеппо мсияюгциеся состав.гяю1Цие определяются затем путе.м решения дифференциального уравиепия (21.31), в.которое надо подставить навдепную функцию смещения (21.36).

Независимость очертания функции смещения Ф (х ) от характера изменетш и места нри-Jюжeння медлещю мепяюитхся виеитих во.здействии гадесь остается в cHjIc, как было и при авто-ко;1ебапиях (глава 19).

OiHiaKo ирпнц1ПН1а1ьным от-личие.м функции смешепия (21.36), определяющей прохождение ме;и1енио меняющихся сш-патов через нелинейную систему при пачнчии выпуждеппых коле-бапий, от функции смеП1епия (19.13) при автоколебаниях является существенная завпси-