Л(0)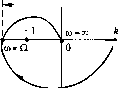

со=0 и

Рис. 6.11

Частотная передаточная функция ра.зомкпутой системы 1У(/ы) отличается от вспо.могателыюй функции WOw) иа единицу. Поэто.му она для устойчивой замкнутой систе.мы не должна охватьн5ать точку с координата.ми г. с. должна проходить так, как показано па рис. 6.11, а.

Если замкнутая систе.ма неустойчива, то в полиноме D{p) появляются сомножители первого или второго порядка с отрицательными коэффициента.ми типа Т,р - 1

или Tfp - 2t,jTjP+l, корни которых положительные или имеют положительные вещественные части. Аргумент, соответствующий перво.му из них (см. табл, 6.1) изменяется от л до -, т. е. на --, а второ.му - иа -л. Если общее число таких корней /,

то им соответствует изменение аргумента D(jti)) на величину -/-. Остальным п - I корням с отрицательной вещественной частью соответствует изменение па величину (н-/). Таким образом, аргу.мент D(;(jo) из.меняется па величину

=-1-+(п-1)- = п-/п.

Аргумент С(;ы) остается прежним: v/2 = п-. Результируюпщй угол поворота вектора W(jй) при изменении частоты от О до о° i(f = - i/2 = -/л. Это означает, что для неустойчивой замкнутой системы годограф вектора IVjOw) охватывает начало координат на угол л/ по часовой стрелке (рис. 6,10, б), а а. ф. х. разомкнутой системы (рис. 6.11, б) охватывает на тот же угол точку (-1;0). В частности, ira рис. 6.10, б и

рис. 6.11, (? угол охвата равен -2п, т. с. в полиноме D{p) имеется два корня с положительной вепюственной частью.

Если замкнутая система находится на колебательной границе устойчивости, то в полиноме D(p) нет корней с положительной вепюствениой частью, но имеется пара чисто мни.мых корней р, 2 - J- граница наиболее характертга для устойчивых в разомкнутом состоянии систем. В этом случае, как следует из выражения (6.16), D(jil) = О, а W(jQ) = -1. Это означает, что на частоте со = Q модуль A{Q.) = 1, а фаза Vj/(i2) = -п, т. е. а. ф. х. разомкнутой систе.мы (рис. 6.11, в) проходит через точку

(-i;jO).

Таки.м образом, если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудгю-фазовая характеристика разомкнутой системы не охватывала точку с координатами ( ~1;;0).

Для случаев, и.зображеииых на рис. 6.11, а - 6.11, в, исходя из критерия Пайквиста можно сформу;1ировать условие устойчивости замкнутой системы. Пусть со = Q - частота, на которой фаза \/(Q) = -п. Тогда замкнутая система будет устойчивой, если .модуль /1(Q) < 1 и неустойчивой, если A{Q.) > 1. При A{Q.) = 1 за.мкнутая система находится па колебательной границе устойчивости, а Q - это частота незатухающих колебаний, возникающих в системе (см. рис. 6.2, г).

Фаза Х/(со), как видно из выражения (6.22), зависит ог значений постоянных времени. Величина модуля, кро.ме того, нронорцнональна коэффициенту передачи разомкнутой систе.мы К. В гл. 7 будет показано, что увеличение К благоприятно влияет на точность системы. Однако одиовремещго увеличивается и .модуль A(Q.). При некотором критическом значении К = Кр за.мкнутая система попадает на колебательную границу устойчивости, а при К > К она становится неустойчи1ЮЙ.

В случае, изображенном на рис. 6.11, г, замкнутая система устойчива при сколь угодно большом значении коэс})фициента передачи разо.мкнутой систе.чнл. Однако практически всегда существуют неучтенные в передаточной функции (6.22) малые

постоянные времени, из-за

чего реальная а. ф. х. разомкнутой системы будет такой, как пока.зано пунктиром, а замкнутая система станет критичной к увеличению К.

На рис, 6.12 изображен более сложный случай, когда замкнутая система может стать неустойчивой как при увеличении, так и при уменьшении коэффициента передачи разомкнутой системы. При Л(йз) < 1, А{0.2) > 1 замкнутая система устойчива. При увеличении К она станет неус-тойчивой, если Л(Оз) > 1, а при уменьшении К - если

А(2) < 1- -(i) 1- Ели же (Q,) < 1, то замкнутая система вновь станет устойчивой.

С;1едует отметить, что если разомкнутая систе.ма устойчива, то устойчив и сам управляемый объект, так как его характеристический полино.м Cq(p) согласно (5.13) входит в состав полинома С(р). Поэтому система автоматического управления со-.здается не для обесиече[Н1Я устойчивости объекта, а для придания систе.ме свойств, отличаюин1Хся от свойств обт)екта, например, для повышения точности поддержания управляемой величины (те\и1ературы, лавле1П1я и т. п.) на заданно.м уровне ири 1галичии возмуще1ШЙ, Однако если алгоритм управления и параметры управляющего устройства выбраны неправильно, то систе.ма авто.матического управления .может стать неустойчивой. Впервые такая ситуация возникла еще в XVHI в. при создании регуляторов скорости враи1еиия валов паровых машин (см. рис. 1.12). И сразу же, как от.мече1го в § 6.2, появшгась необходи.мость в разработке критериев устойчивости.

Сниме.м теперь первое огра1П1чеиие на корпи характеристического полинома разомкнутой систе.мы С(р). Будем полагать, что в не.м кро.ме корней с отрицательны.чи! веп1естве1гными частями есть пулевые корпи, т. е. в выражении (6.22) гО.

При 1ШЛИЧИИ одного пу.,1евого корпя (г= 1) в знаменателе (6,23) появится со-

множитель jti), модуль которого равен ш, а фаза равна -. В результате па частоте w = О модуль частотной передаточной функции разомкнутой системы (6.23) /1(0) = оо, а фаза Vj/(0) = --, т. е. амнлптудно-фазовая характеристика разомкнутой системы будет и.меть разрыв 1геирерывиости (рис. 6.13, а). Для получещгя онределетгости в ходе а, ф. X. замени.м пулевой корепьр, = О бесконечно малым вепюсгвенгнлм отрицательным корпе.м = -а. Тогда вместо;ш получим сомножитель;о) + а, модуль которого

Л)((о) = Voi-a? при (0 = 0 стремится к нулю, а фаза ((о) = arctg-- из.меняется от п

Нуля при ш = О до - при (D->0. При этом модуль (6.23) /4(0) будет стремиться к бесконечности, а фаза будет из.мепяться от нуля до --.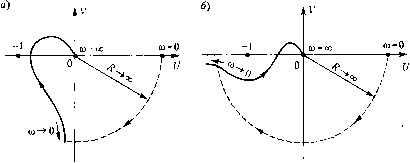