По формулам (22.9) и (22.11) получаем выражения типа (22.13), где

-Ф(м,) + Ф( 2) ,ф<2)=-=(е-

что изображено графически на рис. 22.4, виг.

3. Петлевая релейная характеристика общего вида (рпс. 22.5, а). По фор.мулам (22.7) находим

f = I [Ф(и,) - Ф(М2 ) + Ф(Чз) - Ф( 4)].

где кроме (22.14) и (22.12) введены еще обозначения

т + х< т- X,

Щ =-7. Щ =-р-,

aiV2 а,л/2

Зависимость F/c для случая т =- 0,5 пока.зана на рис. 22.5, б. Далее получаем выражения типа (22,13), где

-[Ф(м,) + Ф(м2) + Ф(Мз) + Ф(и4)1

2 2 J

, -ы, -и., -Ы.7 -ЫТ ч

(е +е +е +е ).

Ф )

0,8 0,6 0,4 0,2 О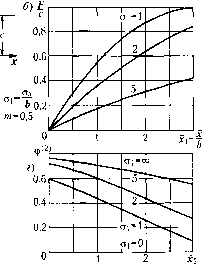

0,8 0.g 0.4 0,2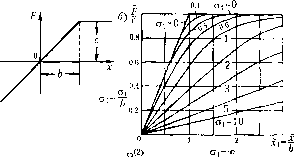

0,6 0,4 0,2

-г-1

Рис, 22.6

Эти функции для случая т = 0,5 изображены иа рис, 22.5, в и г. 4. Характеристика типа насыщения (рис. 22,6, а). По фор.му.че (22,4) с учето.м обозначений (22.12) и (22,14) находим

F .1-, +1

i-, -1

f 2

иг -и, 1 л 2

что показано в зависи.мости от .г, ири разных Sj па рис. 22.6, б. По формулам же (22,9) и (22,11) находим выражение (22,13), где

+ L(1 2 , ,)

Ф(М,)+Ф(М2)-

Нов +ще

что изображено на рис. 22.6, виг.

§ 22.2. Простейшие случайные процессы в нелинейных системах

в данном параграфе рассматриваются такие за/дачи, в которых ре1-улярца>1 составляющая процесса .г (математическое ожидание) постоянна или медленно .меняется во времени но сравнению с составляющими основных частот спектра случайной состав-

ляющсйх. Обратимся к нелинейным системам, динамика которых описывается уравнениями вида

Q{p)x + R{p)F{x,px)-S{p)f{t), (22.15)

где/(t) - внешнее воздействие, прсдставляюп1ее собой случайный процесс, причем

f{t)-f+r{t). (22.16)

Здесь / - заданное математическое ожидание (регулярная составляюн1ая), а/ -

центрированная случайная составляющая.

Пусть пара.метры системы таковы, что автоколебания отсутствуют и система устойчива относительно равтювеспого состояния. Применив статистическую ;ишеари-зацию (22.3) и подставив полученное выражение в заданное уравнение (22.15), разобьем последнее надвауравнения:

Q{p)xR{p)F=S{p)]; (22.17)

[Q{p) + R ip) <7 l.r- = S(p)f\ (22.18)

соответственно для регулярных (математических ожиданий) и случайных (центрированных) составляющих. При этом

f(x,a,.), q {x,a,)

определяются для каждой заданной нелинейности, как указано в § 22.1. Рассмотрим вобн1е.м виде две ра.зличные задачи.

Первая задача. Если имеет место стационарный процесс, то величины f ,х,

аявляются постоянными (имеет место некоторый установившийся режи.м) и уравнение (22.17) принимает алгебраический вид:

Q(0)x + H(0) F(i,a,) = 5(0) /. (22.19)

Здесь фигурируют две неизвестные: х иа. Поэтому в принципе отсюда можно

лишь выразить величину х как функцию а..

д-(а,). (22.20)

Далее по линейной теории случайных процессов, описанной в главе 11, производится исследование уравнения (22.18). В этом уравнении величиназадана спектральной плотностью 5у(ш) или коррашциониой функцией Гу-(т). Линейная теория дает

5(;ш)

Q{jm) + q-RUio)

Sf{i)i)d(ji, (22.21)

где в выражении

дЧх,а,) (22.22)