F(x,px)-1 +дх*+рх* + высшие гармоники,

где при обозначении \\i = ш1

(19.5)

1 ? 2л J

q = - I/(x +asin\/, acocos\/)sin\/rf\/;

it/7 j

, 1

F(x +asm\\i, <2(ocos\;)cos\/<\/.

(19.6)

Отсюда видно, что в обн1е.м случае все три коэффициента являются функция.ми трех иеизвесттях:

/*(х%,(0), (х%,(0), д(ха,ы). (19.7)

В частных случаях эти зависи.мости могут быть более просты.ми. Подстановка выражений (19.4) и (19.5) в заданное дифференциальное уравнение (19.1) с учетом свойства фильтра (см. § 18.2) дает

Q(p){x +х*)+ R(p)\ F° + дх * +рх *

Это уравнение разбивается на два:

Q{Q)x-R(S))f-\

Q{p)x*+R{p)

(О у

х* = 0.

(19.8) (19.9)

При таком разделении сохраняются существенно нелинейные свойства и отсутствие суперпозиции решений, так как остается пелипейная взаимосвязь обоих уравнений через соотношспия (19,7).

Можно предложить два метода решения задачи.

Первый метод состоит в следующем. Уравнение (19.9) совпадает с иреж}!им уравнением (18.33); отличие состоит лишь в том, что теперь коэффициенты д и д согласно (19.7) зависят не только от а и со, по и от смен1ения.г. Поэтому, написав как прежде характеристическое уравнение

Q(P)+H(P)

<? + -Р

(19.10)

С учетом величины смещения первые члены разложения в ряд Фурье вместо (18.6) и (18.7) следует записать в виде

заменивр najco и выделив ветесгвенную и мнимую части, в отличие от (18.36), получим здесь два алгебраических уравнения с тремя неизвестными;

Х{х,а ,ш ) = 0, F(x°,a ,(o ) = 0. (19.11)

Эти уравнения дают возможность определить амплитуду а и частоту со автоколебаний как фуикпии постоянной составляюпюй х :

(х ), со (х ).

(19.12)

Для решения этой задачи можно при.менять любой из способов, описанных в § 18.2, в зависи.мости от того, какой из них лучню подходит к условиям заданно копкретЕюй задачи. Таким же способом можно определить зависимость а и со не только отх*, по и от параметров системы с целью выбора последних. Что касается тех способов § 18,2, где используются графики q (а) и q (а), то здесь их необходимо строить в виде серии кривых при разных постоянных значенияхх (рис. 19.3),

После того как из уравнений (19.11) определены зависимости (19.12), можно, вос-полы )вавн1Ись первым из выражепнй (19.7), найти функцию смещения

f = 0(x ).

Подставив ее в (19.8), получим алгебраическое уравнение

Q(0)x° + 7?(0)O(x) = M

(19.13)

(19.14)

с одной неизвестной х , которая отсюда и онределяется. Чаше всего ;)то уравпение относительно х является трансцендентным и решается графически. Затем согласно (19.12) определяются также амплитуда и частота сОп.

Указанную зависимость (19.12) амплитуды и частоты автоколебаний от величины с.меп1ения центра колебаний надо всегда иметь в виду При одних нелипейностях она можетбыть весьма существенной, при других - .менее существенной.

Второй метод решения той же задачи состоит, наоборот, в том, что сначала реп1ается уравнение (19.8), где согласно (19.7) будет f° (х , а, со) или часто f (х , а). Penienne получает вид

ха.со) или х°(а). (19.15)

Это решепие подставляется затем в уравнения (19.11), которые, таким образом, будут содержать только две неизвестные: и 0) . Определив последние (по любому из способов § 18.2), вычисляем потом по (19.15) и величину х°, которая будет в результате зависеть от (jjopMbi нелинейности, от параметров системы и от внсите-го воздействия М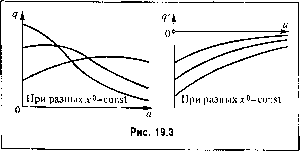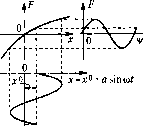

/2(0

Xi Х4

Рис. 19.4

Рис. 19.5

Величинах и является искомой статической или скоростной ошибкой соответственно для статической и астатической систем.

В тех случаях, когда передаточная функ1Н1я линейной части систе.мы R (p)/Q (р) имеет нулевой корень в зна.менателе, т. е. когда Q (0) = О, вместо (19.14) получаем уравнение

Ф(х) =

R(Q)

(19.16)

откуда определяется статическое отклонение или скоростная ошибках (М ).

В случае, когда при отсутствии впеишего во.здействия (М = 0) определяются автоколебания в системе с несим.мегричной пелинейностью, т. е. нелинейностью f (х) или же F (х, рх), для которой

F(asin\\i, аысозц!)с1ц14tО

(19.17)

(19.18)

в.место уравнения (19.8) получаем

Q(0)x + RiO)F

Оно решается любым из тех же двух методов, описанных выше для уравнения (19.8). Одновременно согласно (19.11) определяютсях , а , со .

Если в этом случае знаме1штель Q (р) передаточной функции линейной части системы имеет нулевой корень, то Q(0) = О и, следовательно, уравнение (19.18) с учето.м (19.13) принимает вид

Ф(х) = 0, (19.19)

откуда определяется х . Это означает, что в указанных системах возникает такое с.ме-щениех колебаний переменной х, которое ликвидирует свойственную даппой нелинейности несимметрию колебаний переменной f (т. е. обеспечивается f= 0), как показано, например, на рис. 19.4 в отличие от рис. 19.1,6.

Приведем пример исследования совместного влияния двух внеиших во.здействий, причем из дальнейи1его будет видно, что, в отличие от линейных систе.м, здесь нельзя просто складывать статические ошибки от отдельно взятых во.здействий.