I I---4j-

Т 2Т ЗТ t О

u(i)

Г 2Г ЗГ t 01 Г 2Г ЗУ f

t о

Рис. 15.5

t О

Г 27 ЗГ с

С целью повышения точцости ЦВМ .может быть использована для повьипепия порядка астат1кзма сис темы или реализации комбинированного управлепия.

Повьппепие порядка астатизма, как отмечалось в § 9.1, применяется для устранения устаповивппшся ошибки от задающего воздействия в различных ттювых режи.мах: в пепо/шижиом состоянии, при движении с иостоя1И10Й скоростью, ири движении с постоянным ускорением и т. д. Опо достигается введением в систе.му интегрирующих пли изодромных устройств. Передаточные функции D{z) для их дискретных аналогов ири ведены в табл. 15.1.

В непрерывных системах астатиз.му г-го порядка соответствует наличие сомножителя р в передаточной 4)уикции разомкнутой системы W{p), а в дискретных - и;и1ичие сомножитс;ля (г - 1 )взнамепатеме передаточной фушсции разо.\и<иутойсисте\И)1 W{z), так как каждому корню О соответствует корень2 = е = \ . Поэто.му повышеиие порядка астатизма цифровой системы может быть достигнуто лл счет как непрерывных, так и дискретных интеграторов.

Приициппальная особенность дискретного интегратора состоит в том, что на его выходе образуется не непрерывный сигнал, а последовательность ы(г), что показано на рис. 15.5. Формируюп[ее устройство при у = 1 сохраняет значение в течение периода дискретности 7и образует сигнал и*. Если окажется, что (г) в установившемся режиме изменяется (рис. 15.5, б и рис. 15.5, в), то сигнал и* будет ступенчатым (раз-рывпы.м). Поэтому следует ожидать, что опшбка системы .между \го.ментами замыкания t = Ибуцет иметь пульсации.

Исследуем впача;1е возможность появления нульсацти! исходя из физических соображений.

Пусть имее.м статическую пепрерывиую часть систе.мы и D{z) = 1. Тогда в режиме неподвижного состояния (см. § 8.2) будет су]цествовать постоянная статическая ошибка от задающего воздействия, а м(г) и и* будет изменяться так, как показано иа рис. 15.5, й-Сигналы* непрерывный и появление пульсаций исключается.Дляустраиеиия опИ1бкИ можно нсиолыювать как непрерывный, так и дискретш>1Й интеграторы. В любом из этих случаев u{i) н и* будут такими же по форме, как иа рис. 15.5, а, по при пулевой оишбке.

Для обеспечения режи.ма лвижепия с постояmioii скоростью в систе.ме, как показано в § 8.2, должен иметься по крайней мере один интегратор. Если он непрерывный, то супсествует постоянная скоростная олпгбка, а u(i) и и* изменяются так же, как па рис. 15.5, а, т.е. пульсации отсутствуют. Если жс этот интегратор дискреттяй, то ири постоянной оншбке сигнал и (г) в установившемся состоянии должен изменяться по линейному закону (рис. 15.5, б). При этом сигнал и* имеет разрывный характер, что приводит к появлегиио пульсаций. Таким образо.м, систе.ма может воспроизводить линейно изменяющееся задаюпюе воздействие без пульсаций (но с оиптбкой) только при наличии в ней непрерывного интегратора. Для устранения скоростной оншбки можно использовать дополнптетьно как непрерывные, так и дискретные интеграторы.

Рассуждая аналогично нетрудно убедиться, что для обеспечения движсгшя с но-стоягшым ускорением без нульсагтй в системе должно и.меться не менее двух непрерывных интеграторов. При najunnni одпо1-о непрерывного и одного дискретного интеграторов сигнал W* будет изменяться так, как показано па рис, 15,5, б, а при наличии двух дискретных иггтеграторов - как иа рис. 15.5, о.

Для исследования возможности появления пу.чьсаций можно исполь.зовать также формулу (14,102), Из нес с учетом выражения (14,67) получим

X ,., (е) = 1пп(2-1)

z-->I

G(.,e)-iG(z)

1+IV(2)

(15.26)

Ecjhi окажется, что.г\ .(е) не зависит от е, то и.ульсации отсутствуют, В качестве примера рассмотрим систем}, передаточная функция непрерывной части которой

при наличии дискретного аналога нитсг[)ируютего звена с передаточной функцией

По формулам (14,60) и (14.62) находим;

lV (2,e) = /ciZ::, Щ{г)=К, dik z-d z-d

Передаточныефункцииразомкиутойсистемы(15,10) и (15.9) имеют вид

.z~d-(z-l)d

W{z,e) = Diz)Wa{z,e) = KT W(z) = D(z)W,(z) = Kr

(2-l)(2-J)

(2-l)(2-J)-

В режиме неподвижиого состояния :!ада10Н1ее воздействиеg(f) = Его изображение

G(2,e) = f;(2) = . По формуле (15.26) находим установившуюся онтбку системы

Xy (e) = limgo

(2-1)

z-d-KT(l-d)

(2-)(2-1) + ет(1-)

= 0.

Таким образом, при введении дискретного интегратора статическая ошибка полностью устраняется, что соответствует сделан по.му ранее выводу.

В режиме движения с постоянной скоростью, т. е. upHg{t) = Vt, имеем

G(z,e) = -[l + e(2-l)], G(2) = J%.

(2-1)

Аналогично нредыдуиге.му получаем:

(г-1)

усг(е) = -

1-КТ

\-d \-d

Скоростная ошибка зависит от е, что (как и ожидалось) свидетельствует о наличии пульсаций .между моментами замыкания г = гТ. В моменты вре.мени t = Г/она совпадает со скоростной ошибкой системы при наличии одного пепрерывпого интегратора: дг ( = V/K. На рис. 15.6 это показано для случая Г/Г, = 0,5,ЛГ= 5.

В цифровых системах возможно использование комбинированного управления по задающему или возмущаюгцему воздействия.м. При вынолнегти заданных условий по точности ко.мбипированное управление позволяет снизить требования к основному каналу.

Комбинированное управление особенно удобно применять в тех случаях, когда задаюнгее воздействие вычисляется в унравляюнюн ЦВМ. В этом случае па ЦВМ может быть также возложена задача вычислегиш производных этого возлействия, что

позволяет просто реализовать схемы, аналогичные рассмотренным в § 9.2. Подобное положение возникает, например, при слежении телескопов за планетами, ири управлении но счисляемым координатам и т. Н-Структурная схема системы комбинированного управления для случая использования дополнительного канала с передаточной функцией E{z) но задающему воздействию и.зображепа на рис. 15.7.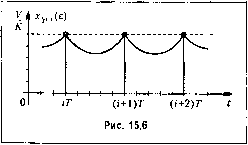