Склонность системы к колебаниям, а следовательно, и запас устойчивости могут быть охарактеризованы максимальным значением управляемой величины г/ , или так называемым перерегулированием

o% = !£2L l<!!l.ioo%,

(8.23)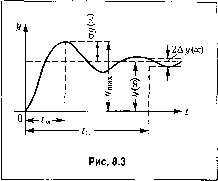

где.г/(°°) О представляет собой установившееся значение управляемой величины после завершения переходного процесса.

Допустимое значение иеререгулирова1Н1я для той или иной системы может быть установлено па осповапии опыта эксплуатации подобных систем. В большинстве случаев считается, что запас устойчивости является достаточным, если величшш перерегулирования не превьипает 10 -ь 30%. Однако в некоторых случаях требуется, чтобы переходный процесс протекал вообп1е без перерегулирования, т. е. был монотонным; в ряде других случаев может допускаться перерегулирование .50 + 70%.

Быстродействие системы может определяться по длительности переходно10 процесса С . Длительность переходного процесса определяется как время, протекающее от момента приложения иа вход ед1нН1ЧПого скачка до момента, после которо1Ч) и.меет местсг неравенство

.г/(0-г/(-)1<А.У(-)-А (8.24)

где Д, - заданная малая постоянная величина, представляющая собой обычно допустимую опшбку; величина г/(о°) в частио.м случае может равняться нулю.

Донусти.мос 31шчепие времени переходного процесса определяется на основании опыта эксплуатации систем управлеиня. В следящих системах в качестве единичного скачка npnnH.viacTCH .мгновенное изменение управляющего во.здействия(/) = 1(f). В этом случае под величиной Л обычно попи.мают некоторую долю входного воздействия, составляюп1ую, как правило, от 1 до 5% величины скачка на входе.

Иногда дополнительно к величине перерегулирования о% (или к величине г/, х) задается допустимое число колебаний, которое .может наблюдаться в течение времени иереходпого процесса. Это число составляет обычно 1 2. В некоторых систе.мах колебания могут вообще не допускаться, а иногда может допускаться до 3 4 колебаний.

Графически требования к запасу устойчивости и быстродействию сводятся к тому чтобы отклонение величины не выходило при единичном вход-но.м воздействии из некоторой области, изображенной на рис. 8.4. Эта область называется областью допустимых отклонений управляемой величины в переходпо.м процессе.

В следящих системах удобно при.меиять сформулированные требования качества к ошибке сп-

i--f----yr-i-zzjiL:-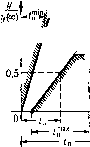

Рис. 8.5

стемы x(t) = g(r) - y{t). В этом случае можно рассматривать область допустимых значений ошибки и при более сложных входных воздействиях, например при мгновенпо.м приложении на входе постоянной скорости.

Дальнейшее развитие критериев качества, использующих переходную характеристику, приводит к введению дополнительных оценок качества (кроме введенных вьнпе f , г/ и а%). К ним относятся следующие оценки.

1. Вре.мя запаздывания Г, равное отрезку времени, заключенному между .момеито.м приложения входного скачкообразного сигнала и моментом времени, при котором осреднепная выходная величина становится равной половине ее установившегося значения. Примененный здесь термин осредне1Н1ая означает, что в случаях, когда на передний фронт выходного сигнала накладываются высокочастотные колебания (это .может иметь место в системах высокого порядка), величина определяется по сглаженной кривой, аппроксимирующей реальную переходную характеристику системы.

2. Время нарастания i , равное отрезку времени, заключенному между точкой пересечения оси времени с касательной, проведенной к осреднеиной кривой переходной характеристики в точке t= t,i\ координатой L точки пересечения указанной касательной с горизонтальной прямой, соответствующей установивше.муся значению управляемой величины. Максимальное время нарастания г ограничивается требуе.мым быстродействием. Миии.мальное вре.мя нарастания ограничивается допустн.мы.мп в системе ускорениями и колебательными режимами.

Уточненная диагра.м.ма качества переходного процесса изображена на рис. 8.5.

§ 8.5. Корневые методы

Как было сказано выше, вид корней характеристического уравнения определяет характер переходных процессов в системе автоматического управления. Поэтому можно cфop.vIyлиpoвaть требования по запасу устойчивости и быстродействию систе.мы, не рассматривая са.мих переходных процессов, а накладывая определегшые условия па корни характеристического уравнения.

Пусть характеристическое уравнение систе.мы имеет вид

+ ... +

+ ... + а ,р + а -

1лер = c+ju) комплексное число.

Используя понятие среднегеометрического корня

(8.25)

PlP2-Pn

(8.26)

где Р2, -. Рп корпи характеристического уравпепия, в формуле (8.25) .можно перейти к новой ко.мплексной величине q путем иодстаповки р = Qq. В результате получим уравнение

q + A,q + ...+Л,/-* + ..,+Л .,+1=0, (8.27)

в котором безразмерные коэффициенты Л . -n-i определяются выраже-

1И1ем

(8.28)

г, - Pi - Pi. а его корпи равны л ~ ~ q и т. д.

Исходное характеристическое уравнение (8.25) при возвращении к прежней комплексной величине получает вид

р +Лйо/ +... + Л4Й[;- * + =0. (8.29)

Среднегеометрический корень может служить .мерой быстроты нротекащщ переходтях процессов. Если в уравнении (8.29) увеличить Ц например, в 10 раз, то на основании теоре.мы подобия (табл. 7.2) переходный нроцссс, оставаясь подобным сам себе, будет протекать в 10 раз быстрее,

В связи с этим .можно рассматривать (8.27) как некоторое нормированное характеристическое уравнение, которо.му соответствует переходный процесс, построенный для безразмерного времени = 0.1. Если качество переходного процесса является нpиeмлeия.м с точки зрения допустимого запаса устойчивости, определяемого, например, перерегулированием (рис. 8.3), то требуе.мая быстрота протекания переходного процесса .может быть обеспечена соответствующим выбором величины Qg,

Для увеличения величины Qq- как следует из (8.26), необходимо увеличиват! свободный член характеристического уравпепия (2 . Напомним, что в статических системах а = 1 -(- if, а в астатических а = К, где К - коэффициент передачи разомкнутой системы. Следовательно, повышение быстродействия может осу1цествляться за счет увеличения коэффициента передачи К. Однако, как уже отмечалось, при это.м у.меньшается запас устойчивости замкнутой системы. В результате переходный процесс (рис. 8.3) становится более колебатсльпы.м.

Для оценки быстродействия системы .может использоваться понятие степени устойчивости .

Под степенью устойчивости г\ 1юцимастся абсолютное значение веществещюй части ближайшего к мни.мой оси корня (рис. 8.6). Здесь могут быть два случая: когда ближайн1ий корень является вещественным (рис. 8.6, я) и когда к мнимой оси ближе всего расположена пара комплексных корней (рис. 8.6, б).

Тер.мип cTeiieiH> устойчивости ие является улачным. и его, вообще говоря, следовало ла.менити термином степень быстродействия . Это объясняется тем, что степень устойчивости никак не спя.чана с уда-.чением системы от границы устойчивости, определяемым по склонности cHCTeNfw к колеба11Иям. Однако . )тот термин ис110Л1>зуется в .читературе, п мь1 будем его иридержн1)ат ься.