кривой (joi) иоиадет в крайнюю точку В (рис. 18.45, г). Это, как видно из чертежа, соответствует такой точке К кривой W, (joi), в которой

Л-,(%)=2--

(18.226)

Из первого условия определяется величина со, и из второго - критическое время запаздывания:

Ч=-\т + Ыщ)] (Рл<0)- (18.227)

Такое решение можно найти непосредственно из гра({)ика W., (jw) или же аналитически, используя выражение (18.220).

Если же реле не и.меет зоны нечувствительности, т.е.Ь= О, то точка В попадет в начало координат на рис. 18.45, г и автоколебания будут при любом значении вре.мени зана.здывания в срабатывании реле (т, = 0). Поэто.му выгодно, чтобы временное запаздывание в реле, рассматриваемое здесь, было бы сравнительно малым, а зона нечувствительности имела бы большую вел1шину (но не превышала допустимых значений, полученных из статического расчета точности регулирования).

Амплитуда и частота автоколебаний при наличии запаздывания определяются следуюшим образом. Точка пересечения D (рис, 18,45. г) дает два периодических решения, так как в ней па пря.мой -М (а) имеются два значения а. Это следует из графика рис. 18.40, а, причем наосновании (18.16) имее.м

что изображается графиком рис. 18.45, д. Расстоянию от начала координат / точки пересечения D па рис. 18.45,гсоответствуютдветочки графика/), иДгиарис, 18.45,Э, которые дают два значения а.мнлитуды: а , и а 2. Частота (0 обоих периодических решений одинакова и оиредетяется точкой D на кривой W., (/ю).

При ;этом периодическое реигсиие с меньшей амплитудой а, будет неустойчивым, а с больпдей амплитудой а 2 - устойчивы.м, так как в первом случае точка с положительным приращением Да налипни -М (а) охватывается кривой И. (jw), а во втором случае - не охватывается. Следовательно, могут иметь .место устойчивость систе.мы в малом (до амплитуд а ,) и автоколебательный процесс с больнюй а.мплитудой, к которому стремится система при начальных амплитудах переходного процесса, превышающих значение а ,.

Заметим, что точку пересечения D кривой W (/со) с линией -Л/ (а) мож1Ю найти без построения кривой W.,., (/со) непосредствепно по амплитудно-фазовой характеристике (joy) линейной части системы без элемента запаздывания. Для этого нужно па кривой (jw) найти такую точку ш (рис. 18.45, г), которая бы при повороте

= 71;

noaie этого находится величина / = Л, а затем амплитуда автоколебаний а 2 по графику рис. 18.45, д.

В заключение заметим, что ири исследовании нелинейных автоматических систем применяются также приближенные .методы Б. В. Булгакова (см. [17] или [701), которые здесь ire и.злагаются.

Глава 19

МЕДЛЕННО МЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ

§ 19.1. Статические и скоростные ошибки автоколебательных систем

в нредылупнгх главах исследовались симметричные автоколебания, как результат свободного движения системы (т. е. без внепшего воздействия) при симметричных пе;нп1ейностях. Однако, как будет показано, важное практическое значение и.меет также рассмотрение несимметричных автоколебаний.

Несим.метрия автоколебаний может вызываться различны.ми причинами: 1) неси.мметричностью нелинейной характеристики как ири наличии, так и ири отсутствии внешних воздействий;

, 2) наличием постоянного или медленно .меняющегюся внешнего воздействия при сим.метрич1П>1х иелинейностях; 3) наличием постоянной или медленно меняющейся скорости измепегнгя внешпе-1-0 воздействия при си.мметричных пелинейностях (для тех случаев, когда постоянное воздействие пе вызывает смещения цеЕггра колебаний; обычно это имеет место в следяпшх системах и вообще в астатических системах).

В само.м деле, если имеется неси.мметричная нелинейная характеристика (например, рис. 19.1, а, б), то даже ири симметричных гсолебагтях переменной х = а sin шг возникают неси.мметричные по амплитуде колебания переменной F(pHC. 19.1, б). Если же нелинейность симметрична (например, рис. 19.2, а, б), то при наличии постоянного внешнего воздействия (или в астатических систе.мах при наличии постоянной скорости из.менеиия внешнего воздействия) смещается центр колебаний переменной X = х -I- а sin шс, вследствие чего колебания перемегшой Рстаповятся несимметричными по амплитуде и по вре.мени (рис. 19.2, а) или только по времени (рис. 19.2, б).

Пусть задана автоматическая система, дииа.мика которой оштсывается уравнением

Q(р)х + R(p) F(x,px) =S(p)/(t). (191)

вектора на угол т(0 попала на липию -М (а), что и даст нам точку D (величиЕШ запаздывания т задана, (0, неизвестна). Условие для определения со будет

а) F

О X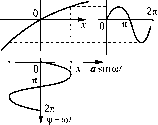

Рис. 19.1

В данном параграфе будем считать f(l) = const =/ для статических систем или же pf (t) = const = /[ для астатических систем. Астатической системой называется такая, в которой .многочлен 5 (р) и.меет общий .множитель р, т. c.S(p)= pS (р).

Поэто.му занищем уравнение (19.1) в виде

Q{p)x+R{p)F(x,px) = M\

(19.2)

где соответственно

Af = S (0)/ или iW = 5, (0) .

(19.3)

При этом решение нелинейного уравнения (19.1), в отличие от прежнего (§ 18.2), ищется в форме

х = X + X*, где X* == а sin cot.

(19.4)

причемx , fl, О) являются неизвестными постоянными.

б) F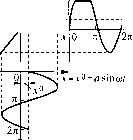

О я

\1 = (йС

v=coC