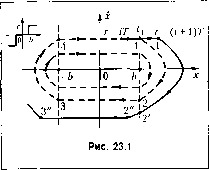или 0. Поэтому, если F(0) = О, то сигнал на выходе нелинейного эвена тоже может п{)инимать одно из трех фиксированных значений: F (И), F(-h) или 0. Таким образом, влияние нелинейности 2 = F (х,) илилз = F{xy,pxy) нри F{0) = О сводится лишь к изменению амплитуды импульсов, что может быть учтено .заранее.

Процессы в пелинейных дискретных системах даже нри отсутствии виеипгих воздействий могут cyniecTBenno отличаться от процессов в пел иней-пых непрерывных системах. В первую очередь это обусловлено наличием квантования но вре.\гени. Влияние квантования по времени иллюстрирует рпс. 23.1, где пунктиром показаны фазовые траектории непрерывной системы, нелинейное звепо которой и.меет релейную характеристику с зоной нечувствительности. В этой системе сунгествуют периодические колебания, амплитуда которых зависит от начальных условий. Реле срабатывает и отпускает при попадании изображающей точки на линии перек.иочспия х=Ь (Т0ЧК1Г 1 и 2) иX = -Ь (точки 3 и А). При данной нелинейности такие процессы будут существовать, напри.мер, в системе, рассмотрен пой в § 17.1 (пример 2).

При наличии квантования по времени в импульсной систе.ме с амплитудги5-им-пульсно!! .модуляцией перек-иочепия реле могут происходить то.тько в дискретные моменты времени t = iT. Это означает (см. рис. 23.1), что в общем случае реле сработает

не в.момент времени (точка У); а в момент t[ +Т] (точка f), где 0<Ti <Г. Соответственно, отиускание реле произойдет не в точке 2, а с заиаздывагше.м по времени па величину 1-2, где О < < 7, причем ф Т] (точка 2 ). Таким образом, система стала неустойчиво!!.

Следует отметить, что в реатьной пе!!рерыв110Й системе тоже су!!сествует;)апазд!)1-вание пр!1 срабат!>!вапии реле т,.р и его от!1усканпи т .,. . Однако величины т и т, зависят от тех!!ических характеристик реле и остаются !!остоян!1!)ГМИ, тогда !сак Т] и Тт

ИЗ.МС!1Я!0ТСЯ в IipOUCCCC работы С!ГСТеМ!)!.

в системах с !иирот!10-нм1!ульс!!ой моду.тяцией !фоцессы будут 1ораздо более стож-иыми, так как в них из.ме1!яется длитель!!ость илп!ульсов.

В пелинеЙ!П)!Х дискретн1.1Х системах нри определенных условиях могут возникать пер1юдическне режимы. В случае их устойчивости они услов!!о .могут рассматриваться какавтоколеба!!ия. Од1шко из-за наличия квантования по вре.мени периодические режимы cy!!iecTBCHi!o отличаются от автоколеба!!ий, определение которых бь!Ло дано в§ 16.1.

Во-первых, частота периодических режи.мов жестко С!5язана с !!ериодом дискрет-

ности Т. Для снм.мегричных режи.мов

N = i2,...,

(23.1)

где Л- относительный нолупериол колеба!!ий. Это означает, что все возможные частоты периодических режимов известпь! зара!1ее.

Во-вторых, при устапов,;1снии периодического режима в сисге.мах, непрерывные части которых содержат интегрируюпще звенья, может появляться постоянная или .медленно изменяк)Н1аяся составляющая они1бки даже ири отсутствии впепншх воздействий и при симметричной нелинейной характеристике.

В-третьих, в одной и той же системе лгогут во.зпикать периодические режи.мы с различными частотами колебаний. При .это.м с течением времени частота может из.мепяться.

Исследование нелинейных дискретных систем представляет собой сложную задачу Ниже будут рассмотрены лини, некоторые подходы к ее репюнию.

§ 23.2. Системы с амплитудно-импульсной модуляцией

с учетом сделанных в § 23.1 допупюпий структурную схе.му нелинейной дискретной системы са.ушлитудпо-пмпульспой \годуляцией .можно представить так, как показано па рис. 23.2, а. Она отличается от изображенной на рис. 15.3 пмичием в ргепрерыв-ной части системы иелипейпого звена с характеристикой щ -F(u). Для простоты возмуп1аюптее во.здействие/(f) здесь пе пока.заио.

Преобразуем исходную схе\гу (рис. 23.2, а) так, как показано на рис. 23.2, б. Очевидно, что если характеристика F(u*) однозначна и f(0) = о, то это всегда возможно. Для нреобра.зованной схемы .можно опредешть передаточную функцию приведенной линейной непрерывной части системы (14.60) или (14.61)

и,(2) Со(2)

(23.2)

и пайти соответствующее ей разностное уравнение (4.11). Если его дополнить ра,зпо-стным уравнением нелинейного звена

щ(1)-Е\иО)], (23.3)

разностным уравнением (15.7), соответствуюгци.м передаточной функции D (z), и урав-нение.м за.мыкания х (г) = g (i) - у (г), то получим систе.му разностных уравнений для замкнутой систе.мы, Рен1ая зти уравнения последовательно щаг за шагом при .заданных внешних воздействиях и начальных условиях можно сравнительно просто исследовать процессы в системе.

Рис, 23.2

Пример 1. Пусть передаточная функция непрерывной части системы \Vq(p) = /sq/p , п\ек = 20с Период дискретности 7= 0,1 с. Передаточная функция приведенной непрерывной части системы (23.2) и.меет вид

Для коррекции динамических свойств системы при.менено дискретное корректирующее устройство, передаточная функция которого

D(2) =

U{z) 2-0,8

(23.5)

х{2) Z

Нелинейное звено и.меет релейную характеристику с зоной нечувствительности:

щ=Р{и) =

csigHM при о при

(23,6)

гдес = 2,й = 0,1.

Задающее воздействиеg (г) = 0, Начальные условия г/(0) = 0,4; г/ (-1) = 0. Запише.м разностные уравнения, соответствующие (23.4) - (23.6):

2signM(0 при u(i) >0.1;

прим(г) <0,1;

u(i) = x(i)-0,8x(i-l); x(i) = gii)-y(i) = -y(i).

Решив эти уравнения последовательно шаг за шагом нри i = О, 1, 2,начиная с последнего, получим процесс, представленный на рис. 23.3. Таким образом, в системе устанавливаются периодические колебания с амплитудой Л = 0,2 и периодом, равным 4Г(отпосительный полупериод колебаний N=2). Частота колебаний (23.1) Q. = я/ 27 .

Заметим, что таким же способом .можно исследовать поведение системы и нри иелиней-ном алгоритме управления и (i) = Ф [-х(г)].

Для исследования устойчивости нелинейных систем с aмнлитyдиo-и.мнyJП5Cнoй модуляцией можно использовать частотный .метод В. М. Попова и метод гармонической липеари,зации.

Первый из них (см. § 17.3) применительно к дискретны.м системам имеет лишь ту осо-

0,6 0,4 0,2

-0,2

Т 2Т

1г/5г 6г J