где че)сзХ2(., Узс и обозначены вещественные и мнимые части соответственно для 04,) и выражения

Ос 04) + 04) \Ч ( в- ь)в. ) +Л(ав. в. ) ] -

Написанное уравнение позволяет определить зависимость амплитуды вибраций ЯцОТ величины полезного сигналах на входе нелинейного звена для каждой заданной вненшей вибрационной помехи (т, е. для заданных В, а) ) графическим приемом, описанным в §21.2 (рис. 21.7).

Полученная зависимость а (х ) подставляется .затем в первую из формул (21.29) для получения функции смещения f ° = Ф (х°), которая в данном случае и будет являться характеристикой нелинейного звена по полезному сигначу Вид ее будет зависеть от заданных амплитуды В и частоты о внешних вибраций и от параметров системы, ВХ0ДЯП1ИХ в выделепную часть контура (рис, 21,13, а).

В обоих рассмотренных случаях, П])Оведя линеаризацию х характеристики нелинейного звена f (х ) или f = сЬ (х ) но полезно.му сигналу, .моЖно обычными методами теории авто.матического управления, исполызуя линейные уравнения (21.44), выявить зависимость всех статических и динамических качеств данной нелинейной систе.мы автоматического управления (и ее устойчивости) от амплитуды В и частоты a),j вибрационных помех.

Линейная система выходила бы из строя при наличии помехтогда, когда полезный сигнал практически перестал бы различаться па фоне помех. Но пока он нормально ра,зличается, все статические и динамические свойства системы по полезному сигналу, если система линейна, остаются неиз.менными, Виб)ациопная по.меха нри зтом накладывается как дополнительная опшбка. Совсем иначе дело обстоит в пелипейпой системе. Коэффттент усиления полезного сигна-ia в нелинейном звене, а вместе с ним и все качества и даже устойчивость системы могут настолько существенно зависеть от помехи (от В и о) ), что система может выйти из строя но этой причине раньше, че.м перестанет различаться полезный сигнал па уровне помех. Это очень важно учитывать на практике.

С точки зрения упроп1ения решепия задачи нужно всегда иметь в виду упрощенную фор.мулу линеаризации (21.45), которая позволяет и во втором из рассмотренных случаев обходиться без определения функции смещения. В этом случае нужно подставить в (21.45) значение амплитуды вибраций на входе нелинейного звена а , найденное нри отсутствии полезного сигнала (х = 0) любым из двух методов, и,з;пшепных в § 21,1, по для более простого уравнения системы (21.51). Зависимость (В) будет при это.м, в отличие от первого случая, криволинейной (рис 21.13, б).

В заключение заметим, что тем же .мегодо.м, что и в § 18.5, легко вычислять высшие гармо1ин<и вынужденных колебаний (см. § 9,4 книги [72]).

Глава 22

СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ

§ 22.1. Статистическая линеаризация нелинейностей

Преднарительно заметим, что по уравнениям, выведенным в § 19.2 и в § 21.2, можно исследовать также медленно меняющиеся случайные процессы в автоматической системе, сопровождаюишеся соответственно автоколебаниями и вынуждеииыми ко-лебания.ми. При это.м целесообразно функцию смещения Ф (х ) подвергнуть обычной линеаризации (19.70) и затем целиком применить линейную теорию случайных процессов к уравнению (19.73) или (21.44). Нелинейная же колебательная часть рещепия определяется с помощью гармо1Н1ческой линеари.зации также, как и в § 19.2 и в § 21.2. При этом находятся сг.тажеппая характеристика (функция смещения) и зависимости амплитуды и частоты колебател1)Ной составляющей от ветчины медленно меняющейся составляющей. В этом случае предполагается, ч то внешние воздействия/(г) в (19.73) и/) {t) в (21.44) являются медленно меняющимися случайными процессами с пормальны.мзакотюм распределения (см. подробнее § 10.1 в книге [72]).

Для реи1еиия других,задач при случайных во.здействиях удобно бьншет при.меиять так называемую статистическую линеаризацию нелинейностей, разработанную П. Е. Казаковым [38]. Сущпость ее заключается в следующем.

Для оценки динамической точности автоматических систем при случайных воздействиях будем определять два первых вероятностных момента случайных процессов: математическое ожидание (среднее значение) и дисперсию (или средпеквадра-тичпое отклонение). Последнее эквивалентно определению спектральной плотности или корреляционной функции.

Если нелинейная система описывается дифференциальным уравнением

Q{p) X + R{p) F(x, рх) = S(p)Kt), (22.1)

то схематически можно себе представить прохождение сигналов, как показано иа рис. 22.1. Проходя через линейную часть, случайный процесс/(?), .заданный двумя первыми вероятностными мометггами, преобразуется в переменнуюх, которую тоже можно определить двумя первыми моментами. Однако определение дальнейшего преобразования случайного процесса х (О в нелинейио.м звене F (х, рх) существенно связано с высшими вероятиостны.ми .момента.ми (подобно то.му как в главе 18 приходилось иметь дело с высшими гар.мониками). Ввиду замкнутости контура системы это обстоятельство накладывает отпечаток и на все процессы в данной системе. Поэтому точное решение задачи в большинстве случаев оказывается недоступным.

Достаточно хорошее для целей инженерных расчетов первое приближепие применительно к рассматриваемым класса.м систем, обладающих свой-ство.м фильтра (см. § 18.2),ластпрепебрсжеииевыс-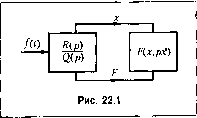

шими моментами, т. е. замена пелипеЙ1и)г0 звена эквивалентным линейным, которое одинаково с данным нелинейным преобразует два первых вероятностных момента: математическое ожидание (среднее значение) и дисперсию (или среднеквадратичное отклонение). Это и называется статистической ;пшеари.зацией нелинейности.

Эта операция по общей идее (но не по конкретному содержанию) аналогична тому, какв главе 19 нелинейное звепо при номопш гар.монической линеари.зации.заменялось эквнватентны.м линейны.м, которое одинаково с данным нелинейным преобразует постоянную (или медлеппо меняющуюся) составляющую и первую гармонику колебательной составляющей, т. е. принимались во внимание два первых члена ряда Фурье и отбрасывались все высише гар.моники.

Итак, представим переменную .г luvi знаком нелинейности F(x,px) в виде

X = 1 - х-, (22.2)

где X ~ .математическое ожидание (среднее значение), которое является обычной (регулярной) функцией времени, их - случайная составляющая с нулевым математическим ожиданием (центрированная случайная функция времени).

Это нредставлениеапатогичнотому, которое употреблялось в главе 19 при гар.монической линеаризации, но оно имеет совсем другой, вероятностный смыс.т. Далее, перемештую f (х, рх) также представим в виде

Р(х,рх) = F + q x-\ (22.3)

где F - математическое ожидание (среднее значение) нелинейной функции/, кото-1К)е является регулярной составляющей; q - эквивалентный коэффициент усиления случайной составляющей (центрировапной).

Это выражение по фор.ме тоже аналогично тому, которое при.менялось в главе 19, по и.меет иное конкретное содержание.

Величина регулярной составляюн1ей F определяется, следовательно, по известной формуле для математического ожидания. В случае однозначной нелинейной функции F(x) ;)та формула дает

F = M[F(x + x )= j F{x + x-)w{x)(bc, (22.4)

где М - обозначение операции взятия математического ожидания, w (.г) - диффереи-ниальный закон расиределения случайной составляющей, например нормальный закон (рис. 11.10):

1 2

хю = --т=е

о,л/2я

(22.3)

Для нелинейности общего вида F{x,px) будет более сложное выражение:

f= F{x л-х, рх + px )w{x, px)dx dpX: (22.6)