Таблица 4.4. Временные характеристики интегрирующих звеньев

Тип звена и передаточная функция

Перехолпая функция

Функция веса

Идеальное

W{p) = -Р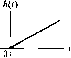

h(t) = к 1(f)

с замедлением

рО+Тр)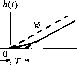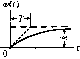

h(t)-k[t-T{l - е-/)]. 1(0

Изодромное

Wip)-Mk,J-,

h(i)

w(t)

h(t) = (kt + k,) i(t)

2. Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением

dt dt

(4.44)

Передаточная функция звена

W{p) =

р(иГр)

(4.45)

Примером такого звена является двигатель (рис. 4.10, а), если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости, к такому же типу звена сводятся демифер (рис. 4.18, б), серводвигатель (рнс. 4.18, в), иитегрируюндай привод (рис. 4.18, г), есди более точно рассматривать их уравнения движения, и др.

Интегрирующее звено с замедлением можно представить как совокупность двух включенных последовательно звеньев - идеального интегрируюп1его и апериодического первого порядка.

Тип звена и частотная передаточная функция

Амплитудно-фазовая

Амплитудная и фазовая

Логарифмические

Идеальное

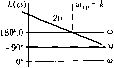Интегрирующее с замедлением k

-кт-

0<-оо

Л(со)

4/{ю)

-90° -180°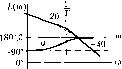

Изодромное

Л(<о)

LV..

90°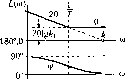

Для нахождения временных характеристик удобно передаточную функцию представить в виде алгебраической суммы

k kT

р(1 + Гр) p \ + Тр

что позволяет представить решение дифференциального уравнения (4.44) в виде суммы реп1ений для идеального интегрирующего звена и апериодического звеиа первого порядка.

Временные характеристики приведены в табл. 4.4, а частотные - в табл. 4.5.

Л.а.х. строится но выражению

Х, = Р

>

Х2 = и 1 1

X2 = U2- u,4-YJu,dt

Рис. 4.19

L(co) = 20lg

(4.46)

Асимптотическая л. а. х. представляет собой две пря.мые с отрицательными наклона.ми -20 дБ/дек (при ш < 1/7) и -40 дБ/дек (при ш > 1/Т). 3. Изодро.мное звено. Звено описывается уравнением

dx.2/dt = kxi + ki dXi/dt. (4.47)

Передаточная функция .звена

wip)Ak, = , р р

(4.48)

где Т= k,/k - постоянная вре.мени изодромпого звена.

Из этих выраже1И1Й видно, что звено можно условно представить в виде совокупности двух звеньев, действующих параллельно, - идеального ицтегрпрующе! о с коэффициентом передачи k и безынерционного с коэффициентом передачи к,.

Примеры изодромиых звеньев изображены па рис. 4.19, Таким звеном может быть комбинация пружины с демпфером (рис. 4.19, б). В качестве входной величины .здесь расс.\гатривается прикладываемая сила F, а в качестве выходной - перемещение х точки а, в которой приложена сила. Это перемещение складывается из деформации пружины

F/C,

где с - жесткость пружины, и перемещения поршня

1/5JF,

где S ~ коэффициент CKopocTnoio сопротивления демпфера. Результирующее перемещение точки

х = Г/с+ l/SFdl.