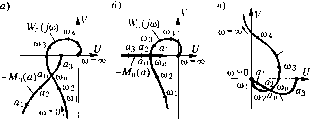to=0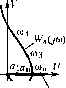

0)1 f 2

М (й)

Рис. 18.41

чепия указанных двух характеристик (рис. 18.41, а и б). В точке пересечения из кривой W. (/ю) бере.\1 значение частоты ю , а нз кривой -М (а) берем ве./1ичипу амплитуды а иско.мого периодического репюпия. Рис. 18.41, а соответствует системе с нелинейным звеном, имеющим гистерезнспую петлю, когда согласно (18,210) и (18,213) характеристика М (а) комплексна. При отсутствии гистерезисной петли, когда М (а) вещественна, получаем график рис. 18.41, б.

Вместо (18.217) можно пользоваться также выражением

(18.219)

т. е. искать peinenne как точку пересечения aHIЛитyдпo-фaзoвoй характеристики нелинейного звена с обратной а.мплитудно-фазовой характеристикой линейной части системы, взятой с обратпы.м знаком (рнс. 18.41, о и г).

Устойчивость найденного иериодического решения грубо оценивается следующим образо.м (этот метод пе является строго обоснованным, по во .многих случаях его применения достаточно). Дади.м .малое приращение а.мплитуде: а = а + Аа. Тогда при положи гельно.м Аа получи.м на кривой - М (а), напри.мер, точку а, (рис. 18.42, а), а при отрицательном Аа - точку Д-чя устойчивости перггодического решения требуется, очевидно, чтобы при положитсльио.м Аа колебания затухати, а прн отрицатель-пом Аа - расходи;п1сь. Для этого согласно критерию Найквиста в случае устойчивой или нейтральной [)азомкпутой системы требуется, чтобы суммарная амплитудно-фазовая характеристика W(a, ю) в нервом случае не охватывала точку (-1, /0), а во второ.м - охватывала. Но общая характеристика W (а, о) ие чертится в рассмотренном

способе. Поэтому высказанное положение надо нерене-стн на свойства кривых W Цш) и -М (а).

Отсюда получаем, что для устойчивости периодического решения (если линейная часть системы в разомкнутом состоянии устойчива или нейтральна) требуется, чтобы а.мплитуд-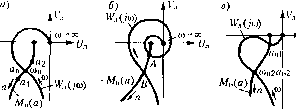

1У (;со) =-

(18.220)

В данном случае очевидно, что обпциЧ знаменатель передаточной функции линейной части системы

Q(p) = (T,p+l)iT+\)p (18.221)

не цмеет корней с положительной вещественной частью, а нулевой корень говорит о том, что линейная часть системы нсйтральпа.

Выражепис, стоящее в квадратных скобках (18.220), при , . = О (система без обратной связи) соответствует апериодическому звену (объект и чувствительный элеме1гг). Оно изображено 1ш рис. 18.43, а. При наличии же жесткой обратной связи в системе (()(. Ф 0) этот график сдвигается вправо на величину k . (рис. 18.43, б).

Множитель перед квадратной скобкой (18.220) соответствует инерциошюму интегрирующему звену (привод с управляющим opianoM). On изображен на рис. 18.43, в.

Перемножением этих характеристик получаем а.хптлитудно-фазовую характеристику (/со) линейной части систе.мы соответствеппо при отсутствии обратЕГОй связи (рис. 18.43, г) и при наличии жесткой обратной связи (рис. 18.43, д). Нанесем наэтиже графики кривую обратной по величине и по знаг v а.мнлитудно-фазовой характеристики -М, (а) нелинейного звена (в данном случае - реле). .Здесь эта кривая изображена в соответствии с рис. 18.39, бд.тя того случая, когда реле характеризуется графиком рис. 18.20, а, причем Ь. = Ь, 6, -- тЬ.

Как видно из рис. 18.43,в данном случае в замкнутой системе без обратной связи воз.мож1Н)1 автоколебания, так как кривые (/m) и ~М (а) пересекаются, а введением

ио-фазовая характеристика липетюй части (/со) не охватывала точку а, соответствующую положительному Аа, и охватывата точку соответствующую отрицател))-ному Аа. По этому признаку графики рис. 18.42, а и б (в точке В) дают устойчивое периодическое решение, которое соответствует автоколебаниям замкнутой систе.мы с частотой со 2, и амплитудой ао-

На грас})ике рис. 18.42, взначения со , и я , соответствуют неустойчиво.му, а значения со 2, [,2 ~ устойчивому периодическому реп1е1Н1ю. Это в простейшем случае может означать устойчивость системы в малом (до амплитуды а ,) и автоколебания с частотой (0,2 и амплитудой а 2, если начальная амплитуда колебаний в переходном ироцессе превыпшет зтшчения а ,.

В таких исследованиях предполагается, что все параметры системы заданы в числовом виде (или амплитудно-фазовые характеристики звеньев в виде определенных графиков). Если же требуется выяснить влияние одного или двух каких-нибудь параметров системы, то надо рассмотреть все возможные комбинации кривых (/со) и -Л/, (а) при разЕ1Е>1х значениях этих пара.метров.

Рассмотрим примеры.

Система автоматической стабилизации температуры. Уравнения систе.мы с релейным звено.м были описаны в при.ме])е .5 § 18.3. Выражение а.мплитудно-фазовой характеристики линейной части системы с добавлением жесткой обратной связи будет

Объект и чувстви- Объект и чувствительны!! тельный элемент элемент с включением

б) Аобратной связи

ю = 0

1ривод

-M(fl)

ю = 0

-мГ(а)

е) 2* 1/

1*2с*

-Мн(а)->

-Мн(а)

Рис. 18.43

обратной свяли .можно уничтожить эти автоколебания (рис. 18.43, д). Очевидно также, что и выборо.м параметров линейной части системы (т. е. деформацией кривой па рис. 18.43, г) можно было бы уничтожить автоколебания замкнутой нелинейной системы и без обратной связи. Напротив, неудачный выбор пара.метров может привести к автоколебаниям системы даже и при наличии жесткой обратной связи, если па рис. 18.43, д кривые пересекутся. Чем меньпю гистерезисная петля (рис. 18.20, а), тем больню будет т (рис. 18.39) и тем легче, как видно из рис. 18.39, б и рис. 18.43, г, д, сделать замкнутую систему устойчивой.

Когда реле и.меетчисто гнстерезисную характеристику (рис. 18.20, г) кривая -Л/ (а) ве)Ерождается согласно рис. 18.39, б (т = -1) в нря.мую (пунктир па рис. 18.43, д), приче.м добиться уничтожения автоколебаний в этом атучае нельзя, а можно бороться лин1ьзау.меньшенрю их амплитуды.

Если в характеристике реле с зоной нечувствительности не будет гистерезисной петли (рис. 18.20, б), то согласно рис. 18.40, а и формуле (18.213) обратная амплитудно-фазовая характеристика нелинейного звена -Л/ (а) будет вещественной, как показано па рис. 18.43, ей ж. При это.м за,мкЕ1утая система без обратной связи может иметь автоколебания, если (/со) примет очертание, показанное нуЕ1ктиром (рис. 18.43, е). Введение же жесткой обратной связи, как видно из рис, 18.43, ж, полеюстью уничтожает автоколебания.

Из этого предварительного рассмотрения .можно сделать вывод, во-первых, о важном стабилизирующем свойстве дополнительной жесткой обратной связи в системе и, во-вторых, о стабилизирующем свойстве зоны нечувствительности реле, С точки зрения устойчивости системы выгодно увеличивать и то, и другое. Однако эти возможности ограничены из-за увели гения статической ошибки системы при усилении жесткой обраттюй связи и при увеличении зоны нечувствительности реле. Последнее связано с тем, что система .может находиться в состоянии раВЕЮвесия в любой точке зоЕН>1 нечувствительности; получается ЕЕе одно определенное состояние равновесия, а целая область возможиьгк состояний равновесия с разны.ми значениями управляе.мой величины.