бирать и любой другой более подходящий нелипей)1ый закон для 01П1сания характеристик двигателя.

Введем для да.П)ейшего обозначение

(18.118)

Тогда дифферетщальное у[)авпеиие двигателя

J dx

dt \+С:

и -с.,х-с

(гдеJ - момент инерции всех вращаемых двигателем масс, приведенных к валу двигателя) можно записать в виде

Здесь имеем три пе.чинейные фу1ПОШи:

h=x\

Гармоническая их линеаризация по правилам § 18.1 дает:

Aadx 8й! 3fl2 г, =--, г.) =-X, 1\=-X.

Подставляя это в (18.119), получаем следуюпюе ypaBneime двухфазного двигателя (для колебательных процессов):

7;5(1 +h,a)p+(1+Ь2а + Ь:а)]х = к:и, вместо обычного линейного (7з/9 + 1)х = з[/,где

T,=J-, k,=\ ft,=i, b2 = 2b,+.

( 2 c2 on dnC2

3£3Q

(18.120)

(18.121)

Здесь a обозначает амплитуду колебаний угловой скорости двигателя х= сОд.

Дааее, скорость пе[)емещеиия управляющего органар с уютом передаточного числа редуктора и с обозначением (18.118) будег

р = (х.

(18.122)

Уравнение объекта и уравнение чувствнтельно10 элемента возьмем соответственно в виде

где ф - отклонение управляемой liejniMnHbi.

X = kk-

ог =0,

(18.125)

7з (1 + ft,a) + ?! (1 + + :(а) К = (1 + 2 + зд )00 - 7;зГ, (1 + й,а)м = 0. Рассмотрим при этом влияние параметра А. Второе изуравпеиий(18.125) дает

b.TJ.ii-Ь2+у1(Ь,Щ(л1 -h,)- 3(737i(of, -1) п - 21) (18.126)

Из (18.121) видно, что 2 i- Поэтому полученная формула дает зависимость амплитуды а от частоты о) иско.мого периодического решения в виде i-рафика, нока-.заниого на рис. 18.23, б, где

0),. =

Р-- (18.127)

Далее, первое из выражений (18.125) при О) = О) и а = а с использованием второго приводит к формуле для парамсгграА, влияние которого рассматривается:

= (1 + ba )(1 + ТМ )o)i. (18.128)

Поэтой формуле, используя предыдущие результаты, получаем фафикзависимо-сти амплитуды автоколебаний а от величины пара.метра к, показа)ПП)ГЙ па рис. 18.23, в.

§ 18.4. Нелинейные системы второго класса

Нелинейные систе.мы второго класса - это системы с нескольки.ми нелинейными звеньями или же с одни.м нелинейны.м звеном, когда иод знаки нелинейных функций входят две или более переменных, свя.занных .между собой линейными передаточными ())ункциями или нелинейными уравнениями. Обычный прием приближеиного решения, излагаемый ниже в при.мерах 1 -3, справедлив при соблюдении условия (])иль-тра, оговоренного в § 18.2, для всех передаточных функций, связываюпнтх указанные переменные. Если это условие i re соблюдается, применяется специальный прием решения, изложенный ниже в примере 4.

Пример 1. В предыдущем параграфе рассматриваюсь влияние нсуншейности привода, а затем влияние квадратичного трения ги) отдельности. Рассмотрим геиерь

Ха[)актеристнчес1<:ос уравнение всей замкнутой системы будет

[7з(1 +6,а)/5 + (1+/;2а + 6;,а)1(ГР + 1)р i- (18.124)

k = kjiji. После подстановкир =j(i> нолучае.м: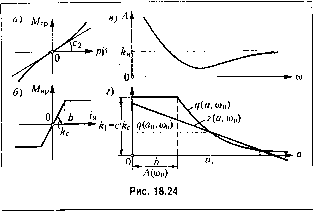

совместное действие нелинейности !1ривода и квадратичного трения. Момент трения нри этом описывается нелинейным членом F(х), как в уравнении (18.90), или, что то же са.мое, графиком на рисунке 18.24, а. Нелинейный !1ривод пусть имеет характеристику типа насыщения (рис. 18.24,(5).

Тогда уравнение двигателя и управляемого объекта вместо (18.90) примет вид

(r,jo+l).r + f(x)= cf,(g, х = рр,

(18.129)

где f 1 (гд) М р и определяется графиком рис. 18.24, б.

В данно.м случае получается нелинейная система второго класса.,Приближенно полагаем, что при автоколебаниях

x = asm(i)l:, = Ааsin (М + В),

(18.130)

где А (0)) и В (0)) - модуль и аргумент ам!1литудно-фа:зов()й характеристики линейной части, !!олучаемой из уравнения (18.67), которое согласно (18.129) надо у.множить на р. В результате получим

Отсюда

(1 + Т,У)ш-

(18.131)

что изображено графически на рис. 18.24, в.

Поскольку в уравнение (18.129) !1еременпые х = и i входят раздельно, то и гармоническую линеаризацию можно производить для каждой из них отдельно. К нелинейности в левой части уравнения (18.129) применяем формулы из прежнего примера 3 (с Авадратичпы.мтреиием),акпелиней юсти в правой части - формулы (18.65) и (18.66), в которых, в соответствии с (18.130), вместо а подставляем Ла. В результате нелинейное уравпение (18.129) прини.мает вид

8kga Зя