в) X2i

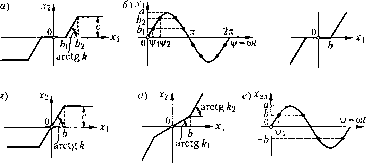Рис. 18.2

где и \\i2 опреде,.1яются формула.ми (18.19). Ввиду отсутствия гистерс.чисиой петли чдссь q = О,

Итак, у])авиение пелипейпого звена с характеристикой вида рис. 18.2, а будет Х2 = q (а).г 1, гдеq(а)оп[)еделяется выражением (18.20).

Как частный случай отсюда получается значение q (а) для звена с зоной нечув-ствителыгостн без насыщения (рис. 18.2, б). Для этого в предыдущем решении нужно

положитьа<Ьи, следовательно, 2 = Тогда

! = k--

. h hi b arcsm-+ -Jl--a a

при a>b.

(18.21)

Как видим, звено с зоной нечувствительности уподобляется здесь линейно.му звену с уменьп1енным за ее счет коэффициентом усиления. Это у.мепьпшние коэффициента усиления значительно при малых амплитудах и невелико при больших, причем О <q (a)<k при < а < оо.

Для второго частного случая - звено с насып1еиие.м без зоны нечувствительности (рис. 18.2, г), - полагая 6, = О, т. е. v/, - О, из (18.20) и (18.19)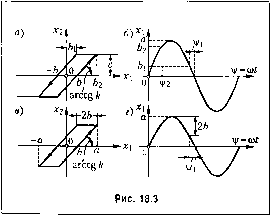

получаем 2k

. с с arcsin-- + -- . ak ak \

при а>-.

J -(18.22)

причем нри а < c/k имеем = (линейная характеристика). При амплитудах колебания входной величины, захваты-

ч = -

,asin\j/sinv[f u?v[f-(--

7t-V2

[k.iasnwi-h) + k\b]?,\u.Mf d\if-\-

ЧТО с .заменой sin v[f, = b дает

q = ko -(2 -i)

. b b h arcsin--(--, 1--a a\ a

при a> b.

(18.23)

Здесь ломаная характеристика (рис. 18.2, д) за.меняется одной прямой со средним между , и 2 наклоно.м q (а), причем этот наклон изменяется в интервале kq (а) < 2 при увеличении амплитуды Л < а < оо. Для а.мнлитуд а<Ь имеем линейную характеристику с наклоном i.

Для нелинейного звена с пасьнцеиием и с гистерезисной нетлей (рис. 18.3, а) уравнение получит вид (18.9), где согласно рис. 18.3, 5 и формула.м (18.10)

(asin \/ - /)),sin V/ й?\)/

7t-V2

(asinv[f -(-i)sinv[f av[f.

аналогично и для q {a). Отсюда

q = - \i/2-(--sin2\/2-(--sin2v[f

%\ 2 2 ,

q = -(sinvi/j-sinij;,) (a>b2),

(18.24)

. bn . c + bk .Л)

ij;, = arcsin- = arcsin-;-, ij;, = arcsin- = arcsin a ak a

. c-bk ak

(18.25)

ваюших зону насыщения, данное звено заменяется как бы линейным звеном с тем меньшим коэффициентом передачи q (а), чем больше амплитуда (в противоположность предыдущему).

Для звена с пере.меииы.\г коэффициенто.м усиления согласно рис. 18.2, д и е но фор.муле (18.10) с учето.м (18.12) получаем

Если в таком нелинейном звене амплитуда колебаний входной величины будет а< Ь, то в процессе колебаний не будет захватываться зона насыщения и получится чисто гистерезисная характеристика (рис. 18.3, в). В данно.м случае

V2 = 2

=arcsin

(18.26)

Уравнение звена с гистерезисной характеристикой вида рис. 18.3, в поэтому будет иметь форму (18.9), где согласно (18.24)

<?=-я

я 1 .

+-sin 24/1

, k 2 kb

q --cos =--

% %a

при a>b.

(18.27)

Величина вычисляется но формуле (18.26).

Такого же типа характеристика (рис. 18.3, в) получалась и для чувствительного элемента с сухим трением в системе стабилизации давления, рассмотренной в § 16 (см. рис, 16.21,6), когдамы пренебрегали массой. Следовательно, для такого нелинейного звена с сухим трением будут справедливы те же формулы (18.27) с заменой в них только

а уравнение (16.58) для колебательного процесса в форме (18.9) будет

11 =

ф-(-высшие гармоники.

(18.28)

(18.29)

Этого же типа характеристика (рис. 18.3, в) имела место и для нелинейного звена с зазором в следящей системе (см. рис. 16.20, б), причем там k = i. Следовательно, уравнение (16,55) данного нелинейного зведга (для колебательного процесса) запишется в виде

qia) +

qXa)

3i -i- высшие гармоники.

(18,30)

гдс<7(а)и (а) определяются по формулам (18.27), в которых надо считать - 1.

Для нелинейностей, гге заданных аналитически, существует графический способ определения q (а) (см, § 3.8 в книге 72]),