..,=щГ., WV.VC=-=-. (12.71,

по фазе (в запретной области) получается максимальным (см. формулу (8.88));

где -Jc соответствует модулю, а -?= - относительной часто-ге, при которых запас

Эти параметры соответствуют митншальному значению показателя ко.чебатель-ности при заданной иротяжепности участка h.

Следует заметить, что технически реализовать систему тем легче, чем меиьП1е протяженность участка h. Это связано с необходимостью подъема на этом участке верхних частот, что во многих случаях затруднено вследствие наличия в системе внешних и внутренних высокочастотных помех. Поэто.му с точки зрения опти.мальнос-ти инженерного решения необходи.мо стремиться к реализации желаемых динамических качеств при .минимальной требуемой протяженности участка h.

Для получения заданного показателя колебательности в замкнутой системе при фиксированной базовой частоте л. а. х. необходимо иметь следующие постоянные времени:

(,2.74:

М + \

Вместо базовой частоты cOq за точку, фиксирующую положение л. а. х. (рис 12. К и 12.11), можно принять, напри.мер, точку пересечения второй асимптоты л. а. х. (

ном выборе параметров, т. е. при совпадении максимумов реальной фазовой характеристики и запретной зоны (рис. 12.11):

= (12-69)

М = ~. (12.70)

/г-1

Эти формулы связывают протяженность участка h с минимальным значением показателя колебательности, который может быть получен при этой протяженности, или величину показателя колебательности М с минимальной протяженностью участка h, обеспечиваюп1ей этот показатель колебательности.

Из рис. 12.11 легко найти оптимальные параметры л. а. х.: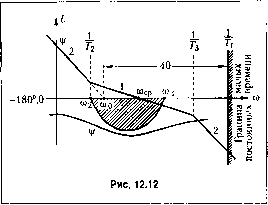

осью децибел, которой соответствует частота со = сОоТг- Тогда вместо (12.73) и (12.74) получим выражения, которые при ({фиксированной часготе среза, а следовательно, и с{)пксировапном положении запретной зоны для фазовой характеристики можно превратить в неравенства:

1 М

При равенстве левых частей правым показатель колебательности будет равен за-данно.му значению М. При неравенстве левых и правых частей будет вводиться некоторый дополнительный запас устойчивости и показатель колебательности будет снижаться.

Эти формулы легко запоминаются, и oini просто связаны с параметрами окружности - запретной зоны на ко.мплекс1ЮЙ плоскости (см. рис. 8.22).

В неравенство может быть превращена и фор.мула (12.74). Формулу (12.73) лучше иметь в виде равенства, так как увеличение по сравнению с те.м, что дает фор-Myjra, в некоторых случаях может привести к ухудшению запаса устойчивости.

При использовании типовой передаточной функции (12.62) может быть предусмотрен дополнительный запас устойчивости для возможности иметь в усилительном канале некоторое количество не учитываемых при расчете малых постоянных времени. Донолнителььнлй запас устойчивости создается уменьшением величины постоянной времени Tj или, соответственно,

13 =

чтобы отодвинуть фазовую характеристику от запретной области (рис. 12.12).

Па .малые постоянные вре.мени отводится обычно несколько градусов запаса по фазе. Так, ifanpn.Mep, в [9j предлагается отводить на эти цели величину, соответствующую сумме .малых постоянных.

(12.77)

а число малых постояшпях времени принимать равным 4 + 6. Тогда граница малых постоянных времени определяется значением

ZM 0,025 ~ 4 - 0)0

(12.78)

Если некоторая постоянная времени дает сопрягающую частоту (л = 1/ Г, которая больще граничной частоты (рис. 12.12)

О), = 1/7; = 400)0. (12.79)

го эта постоянная может не учитываться при расчете.

Расчетная формула для определения допустимого значения постоянной времени Г2 (12.73) при этом сохраняется, а вместо формулы (12.74) должно использоваться выражение

©о

fVM(M-i)

M-t-l

(12.80)

В более сложном случае передаточная функция разо.мкнутой системы может и.меть произвольное число постоянных вре.мени, входящих в ее зна.менатель;

W(p) = ---. (12.81)

p\\ + T,p)iUT,p){\ + r,p)...

Этой передаточной функции соответствует л. а. х. типа 2-1-2-3-4...

Расчеты и здесь оказываются достаточно простыми. Для получения заданного показателя колебательности необходимо выполнение условия (12.73) для постоянной времени Т2. Су.мма всех остальных постоянных времени 1Г= Г3 + + + -. включая ма.тые постоянные времени, должна удовлетворять неравенству

УТ±ШЕ. (12.82)

Юо + 1

При использовании расчета по частоте среза для ностоЯ1ГИОЙ времени 72 должно выполняться условие (12.7.5), а для суммы остальных ностояггпых времени - условие

УТ<~-(12.83] щМ + 1

В л. а. x. подобного типа легко учесть наличие звеньев постоянного запаздывания. В этом случае время запаздывания должно учитываться при подсчете су.ммь постоянных вре.мегги ИТ.

Воз.можен случай, когда в передаточную функцию разо.мкнутой системы входит множитель, соответствующий колебательно.му звену с комплексными корнями:

W(p) = --А + Т-Р- (12.84

р\\ + Цр)(1 + ар + Ьр)...