Введем обозначение для скорости изменения отклонения управляемой величины

у ~ -L Тогда уравнение системы (16.23) преобразуется к виду

- = -ау-а2Х, dx

Tt--

(16.24)

Исключим из уравнений (16.24) время С, ра.зделив первое из них па второе (прих и г/ 0):

= -а,-а,-. (16.25)

dx у

Решение г/ = ф(х) этого дифференциального уравнения с одной произвольной постоянной определяет собой некоторое семейство так называемых интегральных кривых на фазовой плоскости (х,.г/), каждая из которых соответствует одному определепно.му значению произвольной постоянной.

Вся совокупность интегральных кривых представит собой все возможные фазовые траектории, а значит, и все возможные виды переходного процесса в даппой систе-e при любых начальных условиях.

решение дифференциальных уравнений возмушенного движения (переходного процесса) удовлетворяет неравенствам

!.г,(01<е, (г=1,...,и)

при любом сколь угодно больпюм t, начиная с некоторого t=T> 0.

Представим себе для этой аналитической записи геометрический образ в фазовом пространстве. Очевидно, что при ограничении начальных условий по каждой координате неравенствами (16.22) получается и-мерпый параллелепипед со сторонами 2ri внутри которого должна лежать начальная точка фазовой траектории Mq (.г, x2q, х о). На фазовой плоскости (п = 2) он обрап1ается в прямоугольник. Аналогично и второе из написанных неравенств гео.метрически означает, что фазовые траектории не должны выходить из парачлелепипеда со сторона.ми 2е,.

В формулировке Ляпунова содержится требование сколь угодной малости ука-за1П1Ых областей. Однако практически это определение, так же как и теоре.мы Ляпунова, которые будут приведены ниже, при.меняется и тогда, когда эти области имеют определенные конечные раз.меры.

Фазовые траектории для обыкновенных линейных систем. Пусгь переходный процесс в некоторой системе описывается уравнением второго порядка

dl + a, + a2X = 0. (16.23)

dt dt

Рассмотрим отдельно различные случаи. Уравнению (16.23) соответствуют корпи характеристического уравнения

причем возможны пюсть случаев:

1) KopiHi чисто мнимые при а, = О, 2 > О (колебательная граница устойчивости линейной системы);

2) корни комплексные и и.меют отрицательные вещественные часгиири cij <Аа2,

А, > О, (h > о (устойчивая линейная система);

3) корпи комплексные и и.меют положительпые вещественные части ири ci < Аа.), а, < О, 2 > О (неустойчивая линейная система);

4) к01н1и веиюствепные отри11ательпые при < 4а2, а, > О, 2 > О (устойчивая линейная система);

5) корпи вещественные положительные при af <4fl2. а-< О, 2 > О (неустойчивая линейная система);

6) корни вещественные и и.меют разные злаки при а-) < О (неустойчивая .яинейная снсте.ма); в частности, один из корней будет равен нулю при а2 = О (апериодическая rpaimna устойчивости линейной систе.мы).

Случай 1.В перво.м случае получаются, как известно, незатухаюниге колебания (рис. 16.8, а)

х = А sin ((Of + Р), у cos (юг г р), ш = Г.

(16.26)

с постоянной амплитудой А и начальной фазой (3, которые зависят от пачалыпях условий. /1ля фазовой плоскости уравнения (16.26) представ.чяют co6oii парамет1)ические уравнения .эллипса с полуосями/1 исоЛ (рис. 16.8,6). Уравтюппе .эллипса

а) о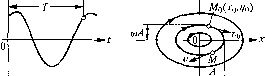

- = 1

Л {(НАУ

можно получить непосредственным ре1нение.м дифференциального уравнеппя фазовых траектории (16.25) при а, = О и а, = причем А -- П1Юизвольная постоянная интегрирования.

Итак, псриодич(;ским колебаниям системы (1)ис. 16.8, а) соотвегствует движение изоб-ража10П1ей точки ноза.мкпуто!! кривой (рис. 16.8, б).

С .I у ч а й 2. В это.м случае (комн.тексные корни с отрипа-тельпыми веп1ествепнымп частя.ми), как известно, имеюг место затухаюппи; колебания(рис. 16.9, а)

а) X

У-Рх,

Щхо.уа)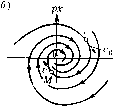

Рис. 16.9

X = Ле sni(co/ г Р), г/ = -- = уАе cos(M -ь (3 -ь 5),

а-, -

Y = 7 7. 5 = arctg-,

а произвольные постоянные Л и (3 определяются пз начальных условий:

л=до, у=Уо= х при 0.

Значениях и у не возвращаются за период колебания к прежним, а становятся меньше. Это дает на фазовой плоскости (х,у) кривую (рис. 16.9, б), которая за один оборот не возв1)ап1ается в прсжикно точку Mq, а подходит ближе к началу координат.

Итак, затухаюн1им колебаниям систе.мы (рис. 16.9, а) отвечают фазовые траектории в виде спиралей, по которььм изображающая точка приближается к началу координат (рис. 16.9,6).

С л уча й 3. Этот стучай (ко.\и1лексные корни с положительными вещественными частями) соогветствует расходящимся колебаниям (рнс. 16.10, а). Рассуждая аналогично предыдущему, получим вск5 совокупность возможных фазовых траекторий тоже в виде спиралс!!, но только изображающая точка будет двигаться но ним не к началу KooivuniaT, а от него (рис. 16.10, б).

С л у ч а й 4. Этот случай (вещественные отрицательные корпи) соответствует апериодическому процессу