которое для петлевых нелинейпостей 1{х) ири симметричном .чаконе распрел(>леиия (в том числе и нор.ма.тьио.м) упрощается. Например, для нелинейности, [пжазапной па рис. 22.2, будет-

F= j F(x + x- )x0(x)dx+ j-\F(x + x )+F2(x + x )]wix)dv +

(22.7)

F(x + x )w(x)dx.

Величину эквивсиюптного коэффициента усиления q случайной составляюп1ей в формуле (22.3) реко.меидуегся определять одним из слсду1оип1х двух способов.

Первый способ исходит непосредс гвенпо из всътичин среднеквадратичных отклонений а,- и Ор переменной .г и нелинейной (1)ункции F, а именно:

а,1л/Кх )] что в случае однозначной нелинейности F(x) дает

)да(л-)й[1-Я.

(22.8)

(22.9)

Для общего случая F(x, рх) и в случае петлевой нелинейности F(x) получаются более сложные выражения, которые можно получить д.тя 9 , обобщив (22.9) по тому жс образцу, как обобщены выражения (22.6) и (22.7) по сравнишю с (22.4).

Второй способ заключается в определении коэффициента q из условия миниму.ма математического ожидания квадрата разности истинной нелинейной функции F (.т, рх) и ее заменяющей (22.3), т. е. минимума среднеквадратичного отклонения. Записав это условие

M{[F(x,px) - F q x f } = min.

получим

М[(х-)2

(22.10)

где Гр - значение взаимной корреля1и101П1ои функции переменных f их при т = 0. Отсюда в случае однозначной нелинейности F (х) находим

F(x + х- )х~г<у(х) dx. (22.11)

Рис. 22.2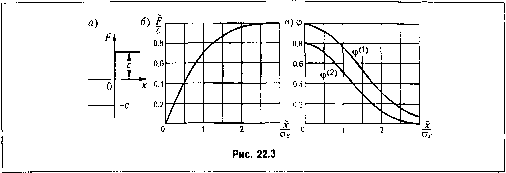

Аналогично предыдущему легко получить также выражетте коэффициента (f для общего случая f (х, рх) и для петлевой нелинейности F(x).

Второй способ определения коэффициеита 9 приводит к более простым расчетным формулам. С этой точки зрения его использование предпочтительнее. Поточности же оба способа примерно равноценны и соответствуют общей степени приближенности всего .метода в целом. Замечено, что во многих случаях, когда первый из этих способов дает завышенные значения корреляциоипой функции пелипейпого процесса f (t) по сравнению с точны.ми, второй дает занижен(п>1езначе1щя. Поэтому часто может получиться более xoponiee приближение, если в качестве величины взять среднее арифметическое из двух; (22.8) н (22.10).

Важно иметь в виду, что величины F w q в.заимосвя.запы тем, что каждая из mix :!авнсит от обеих 1)ассматрнваемых характеристик случайного процесса: х и а. (входящих в закон распределения w). Сам факт наличия этих зависимостей и их взаимосвязь позволяют, несмотря на линеаризацию задачи, уловить существешю нелинейные особенности случайных процессов, подобно тому как в прежних главах ;5ависимость величин qviq от всех трех неизвестныхх , а и о) (или по крайней мере от первых двух из них) и взаимосвязь этих величин позволяли исследовать существенно нели-пейш>1еособе1П10сти регулярных процессов во времени методом гар.монической линеаризации.

Приведем выражения величин F и г/ и их графики для некоторых типовых нелинейностей, составленные по формулам (22.4), (22.9) и (22.11) нри условии нормального закона распределения (22.,5) случайной переменной х (нри других законах распределения величины F и с/ имели бы другие выражения).

1. Идеальная релейная характеристика (рнс, 22,3, а). Из формулы (22,4) находи.м

Р = сФ(и), и =

а,72

где обозначено

Ф(м) =

2 г 2

е dy

(22.12)

(числовые значения этого интеграла вероятностей имеются в справочниках, а также приведены в табл. 11.2). Завнси.мость величины F/с от отнондения х/о,. показана графически на рис. 22.3, б.

По формулам (22.9) и (22.11) находим соответственно

9 =-Ф (х,а,)

9 =-ФЧх.а,), а.

(22.13)

Ф<>=71-Ф(м), ф(2> =

л/2к

Зависимости ф и ф показаны па рис. 22.3, в.

2. Однозначная релейная характеристика с зоной нечувствительности

(рис. 22.4, а). По формуле (22.4) с учетом обозначения (22.12) находим

и, =

1+Xi

a,v2

1-х,

X, =-

(22.14)

Функция f/с изображена графически на рис. 22,4, б в .зависимости от х, нрн разных значениях а,.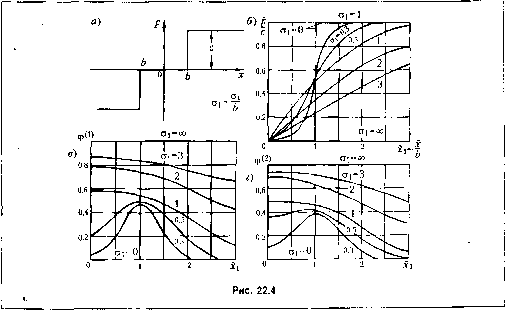