щнх воздействий = /,о, ЛСО = Ло и т. д. Этот режим имеет смысл только в следящих системах и системах программного управления.

Используя изображения Карсопа-Хевисайда, в этом случае получаем G(p)

F,(0=/io. 2(0 =/20 и т. д.

Из общего выражения для ошибки посредством теоре.мы о конечном значении может быть найдегга установившаяся ошибка в это.м режиме:

i+W(p)

(8.5)

Второе слагаемое этого выражения дает статическую ошибку (при условии, что возмущающие воздействия такие же, как в неподвижно.м состоягнги системы), в которой может быть также учтена ошибка чувствительного элемента.

Первое слагаемое (8.5) и.меет с.У1Ысл только при астатизме первого порядка, т. е. в том случае, когда передаточная функгшя разомкнутой систе.мы может бьггь представлена в виде

K~iP+-+Кр )

Р(1 + С .2Р + - + СоР ~)

где Kj, = К - ко.эффициент передачи разомкнутой системы, называемый добротностью по скорости.

Тогда выражение (8.5) приводится к виду

(8.6)

Таким образом, в этом тииово.м режиме установившаяся ошибка будет слагаться из статической ошибки и добавочной скоростной ошибки, равной отношению скорости задания к добротности системы но скорости:

(8.7)

Так как систе.ма .может двигаться с различными скоростями, то качество ее удобнее характеризовать не са.мой скоростной ошибкой, которая является переменной величи1Гой, а значением добротности ио скорости

К,г/х- (8.8)

В статических систе.мах первое слагаемое (8.6) стремится к бесконечности; при астатизме вынге первого порядка .это слагаемое стремится к нулю. Поэто.му режим движения с постоянной скоростью используется для оценки точности только систем с астатизмом первого порядка, главны.м образом следящих систе.м, для которых такой режим является характерным.

Хуст

1.Щ(р)Ло

l + W(p)

(8.9)

/)-->0

Второе слагаемое (8.9), как и ранее, дает статическую оигибку. Первое слагаемое (8.9) имеет смысл только при астатизме второго порядка, когда ггередаточная функция разомкнутой системы может быть предсгавлепа в виде

цгру. клиь, ,р + ... + ь,р )

р\ + Сп-зР + - + СоР ~)

где К = К - коэффиниетгг передачи разомкнутой системы, называемый добротностью по ускореггию.

Тогда выражение (8.9) приводится к BHZiy

Первое слагаемое (8.10) ггредставляет собой добавочную ошибку от постоянного ускорения. Как и в предыдупюм случае, качество систе.мы может быть оценено величиной доб1ютпости по ускорению

Л; = еАу. (8.11)

Этот типовой режим используется только для систе.м с астатизмо.м второго порядка, г.тавпы.м образо.м следящих систем.

4. Движение по гармоническому (синусоидальному) закону. Такой режим используется весьма часто, так как он позволяет наиболее hojhk) оцепить дипа.мичес-кие свойства системы управления. Задающее во.здействие припимается изменяюпщм-ся по закону

,ЧО=& ах- со,г. (8.12)

В зависимости от конкретного вида систе.мы во:!.муП1аюип1е воздействия в рассматриваемом режиме могут оставаться постоянными пли мепят ься.

Случай постоянства возмущающих воздействий приводит, как и в рассмотренных выше типовых режимах, к появлению некоторой постоянной ошибки х .

3. Движение с постоянным ускорением. F3 качестве третьего типового режима используется режим устаповивтегося движения системы с постояпт.ьм ускорением е = const. В этом случае задающее воздействие меняется по закону g(t) = Воз-

мущающие воздействия принимаются постояппы\п1, как и во втором типово.м режиме. Этот режим и.меет смысл только в следящих системах и систе.мах программного управления.

Аналогично изложенно.му выше, установившееся значение ошибки в этом режиме может быть найдено из выражения

Do;iee вероятным является случай, когда возмутаюпцю воздействия ири движении системы в этом режиме меняются во времени. .Это обТ)Ясняется тем, что при движении по гар.моническому закону не1Грерывно будет меняться направление движения системы, а следовательно, одновременно будет меняться направление действу-ЮН1ИХ в системе сил сухого тре1сия. Этот случай является довольно сложггым, и он может рассматриваться только в гцжложеиии к конкрет11ым системам. Рассмотрим ошибку, определяемую только первым слагасмы.м выражения (.5.19):

г = -

\ + W(p)

(8.1.3)

В линеаризованной системе ири гармоническом задаюше.м воздействии (8.12) о/1/ибка в усталовивпге.мся режиме будет также меняться по гармоническому закону с частотой щ:

х = х $т{щ1. + \\1). (8.14)

Точность системы в это.м режиме .можетбыть octenena по амплитуде онп1бки, которая может быть пайле/ia из (8.13) на ос/юва1И1И си.мволнмеского метода подстановкой р =70):

(8.15)

Так как предполагается, что а.мплитуда оншбки значительно меиьпю амплитуды входного воздействия: <?Cg, , то, следовательно, модуль знаменателя (8.15) значительно больше елипиг1Ы. Это 1созволяет с большой точностью выражение (8.15) за.ме1И{ть приближе1игым

W(M) Л((о,)

(8.16)

где Л(со) - модуль частотной передаточной функции разомкнутой системы при ю = ю.

Последняя формула позволяет легко вычи-стять а.милитуду опп1бки в устаповившемся режиме. Для этого необходимо располагать либо агса-литическим выражением для иередаточной функции разо.мкнутой системы, либо и.меть экспериментально снятую амплитудно-фазовую частотную характеристику разомкнутой системы.

Формула (8.16) широко используется также при расчете систе.мы .методом логарифмических амплитудных частотных характеристик (л. а. х.). В этом случае модуль (со) в децибелах, т. е. i((Oi) = 20 Ig Л((0), равен ординате л. а. х. при частоте со = со, (рис. 8.2, а).

Простота выражения (8.16) позволяет легко решить обратную задачу, т. е. сфор.мулировать тре-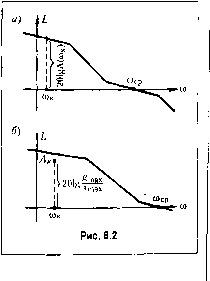