где 1У (/ш) ~ частотная передаточная функция разомкнутой системы.

Максимальное значение этого модуля и представляет собой показатель колебательности (и.меется в виду наибольший максимум)

Л/пшх = ф(; )

и(;ш)

(8.82)

1 + ( , ..

Как видно из этих рассуждений, показатель колебательности определяется посред-cTiiOM задания зада10п1его воздействия g g ,. , sin Ш.. В принципе возможно определение поюиателя колебательности системы посредством задания возмунхающсго во,здей-ствия/ = /тах отыскэния относитсльпой всличипы рсзонаисиого пика.

Чем меньше запас устойчивости, тем бо.тьше склонность системы к колебаниям и тем вьпне резонансный пик. Допустимое значение показателя колебательности определяется па основании опыта эксплуатации систем управления. Считается, что в хорошо демпфированных системах пока.затель колебательности пе должен превосходить значений 1,1 1,5, хотя в некоторых случаях можно допускать величины до 2 2,5.

Для отыскания показателя колебательности пет необходимости строить амп.ти-тудпую частотную характеристику (рис. 8.19) или отыскивать максимум (8.82). Существуют приемы, П03В0ЛЯЮН1ИС найти показатель колебательности по виду амгиш-тудпо-фазовой характеристики разомкнутой системы. Возьмем на а.мп.титудпой характеристике (рис. 8.19) некоторую точку а, которой соответствует ордината М, и отобразим эту точку иа комплексную плоскость частотной иередаточной фупкгцти разомкнутой систе.мы. Для этого рассмотрим уравнение

modO(;co) =

W(;a))

Сделаем подстановки U = Rc 1У (/со) и У = Im W Тогда

U + jV

\+и+jV

-=м.

(8.84)

(8.85)

Это есть уравнение окружности с раднусо.м Яи с цент[)о.м, смещенпы.м влево от начала координат на величину С.

Возводя в квадрат правую и левую части и освобождаясь от знаменателя, после алгебраических преобразований получим

(U+Cf + V = R\ (8.83) I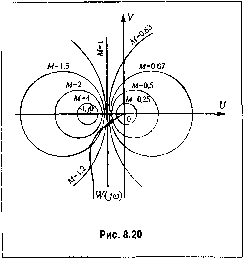

Задаваясь различными значениями М от 1 до °°, можно построить семейство таких окружностей (рис. 8.20). На каждой окружности написано значение ординаты амплитудной частотной характеристики. При М = I окружность вырождается в прямую линию, параллельную оси ординат и проходящую слева от нее па расстоянии 0,5. При М-> о° окружность вырождается в точку, совпадающую с точкой (-1, /0).

Для значений ординат амплитудной характеристики, лежап1их в пределах О < М< 1, получается семейство окружностей, расположенных справа от линии М = 1, симметрично с первым семейством. При М = О окружность вырождается в точку, совпадающую с началом координат. Для построения амплитудной характеристики (рис. 8.19) достаточно в тех же координатах, где построены окружности М = const, нанести амплитудно-фазовую характеристику разомкнутой системы. Точки пересечения этой характеристики с окружпостя.ми будут определять точки амплитудной характеристики с соответствующими значениями ординат, рав1И)ШИ М. Для определения показателя колебательности можно не строить а.мплнтудпую характеристику, так как достаточно знать одно максимальное значение ординаты М, определяемое по наименьщей окружности М = const (М 1), которой коснется а.мпли-тудно-фазовая характеристика.

Если при проектировании систе.мы ставится условие, чтобы ее показатель колебательности был пе больше некоторого заданного значения, напри.мер М. = 1,5, то для выполнения этого необходимо, чтобы амплитудно-фазовая характеристика не заходила в область, ограниченную соответствующей окружностью (рис. 8.21). Лмп-литудио-фазовая характеристика .может только коснуться этой окружности. В это.м случае показатель колебательности будет как раз ранен заданному значению М ,-

Таки.м образом, окружность jVf, j ограничивает запретную зону для амплитудно-фазовой характеристики разомкнутой системы. Эта зона охватывает точку (-1,;0) и обеспечивает получение заданного запаса устойчивости.

Величина показателя колебательности .может быть определена и в случае использования логарифмических частотных характеристик. Для этого отобразим запретную зону (рис. 8.21) па логарифмическую сетку Рассмотрим отдельно окружность заданного показателя колебательности (рнс 8.22).

На окружности возь.ме.м произвольную точку В и построим вектор, соединяющий эту точку с кача-

г, -Ж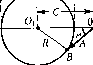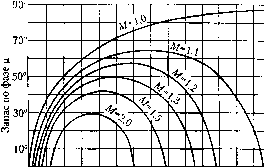

Рис. 8.22

-40 4 8 12 16 20 Модуль в децибелах

Рис. 8.23

ЛОМ координат. Установим для этого вектора связь между его модулем А и запасом по фа,зе р. Из треугольника ОБО, но теоре.ме косинусов находим

Далее можно иайти

и окончательно

р = arccos-

2АС

(8.86)

Из рис. 8.22 нетрудно видеть, что зависимость (8.86) существует только для модулей, лежащих в пределах

М , М <А<-

(8.87)

Ь случае, когда А<--- или А>----, запас по фазе может быть люоы.м, так M-v\ М-1

как в этом случае конец вектора ие может попасть в запретную зону (рис. 8.22).

Задаваясь различнььми значениями показателя М. = const, а следовательно, и С = const (8.84), но выражению (8.86) .можно построить графики р =/(Л), которые носят название [i-кривых. Эти графики строятся обычно таки.м образом, что модуль А откладывается в децибелах (рис. 8.23).