Таблица 10.2

Название и схема звеиа

Передаточная функция

Параметры

Д11ф()сриниируЮ1цес

1 + 7>

с, С1+С2

интег-рирующсс

7; =

.i 2;

s; 7-2=-;

c,+C2

интегро-дифферелцируюнке

Члллл-

ЛЛЛЛ.

<;2

(1 + Г,р)(1+Г2р) (1 + 7зР)(1+7:,р)

3.4 - x

V (7;+a7-2)J

§ 10.3. Параллельные корректирующие звенья

Как уже отмечалось, параллельные корректирующие звенья удобно примепятт! ири использовании сложных алгоритмов управления, когда наряду с основным сиг-нало.м вводятся его производные или интегралы.

Введение интегралов преследует цель снижения установившейся оин1бки. Этот вопрос был рассмотрен в главе 9 в связи с повышением точности систем автоматического управления посредство.м использования изодром1ГЫХ устройств.

Введение производных преследует обычно цель обеспечения устойчивости. В этом случае используются звенья дифферегщирующего типа, включаемые пара-т-лельпо основной цеип.

Варианты параллельного вк.иочепия дифференцирующих звеньев нока.заиы на рис. 10.6. Получение производной второго порядка при помощи одного звеиа является затруднительным. Поэтому схема, изображенная иа рис. 10.6, б используется

hp -

TiPb

Рис. 10.6

редко. Введение второй производной доиолните.чьно к первой производной осуществляется обычно по каскадны.м схемам, изображенным иа рис. 10.6, в и 10,6, г. Для первой из них (рис. 10.(), е) результирующая передаточная функция бу,чет

W{p)=]. + -l\p + TJ.,p\ (10.18)

а для второй (рис. 10.6, г) -

V(p) = 1+(/,+ 7-2)/; +У, V. (10.19)

На рис, 10.6 дифференциаторы изображены идеальны.ми. Волее вероятно, что они будут представлять собой дифференцирующие звенья с замедлением (рис. 4.24).

Замети.м, что введение параллельных корректируюнтх звеньев, представляющих собой интеграторы, соответствует 1К)днятию inminix частот. Это хороню видно па рис. 9.6. Введение паралле;н.пых корректирующих звеньев, предсгавляюптх собой дифференциаторы, соответствует поднятию верхних частот. Это можгю видеть из фор.мул (10.18) и (10,19),

В качестве примера па рис, 10.7, а изображен случай введения дополнительно к основному сигналу, пропортюпально.му углу поворота вала, сигналов, пропорциональных первой и второй производным угла поворота. Первый сигнал Mj вырабатывается датчиком угла - нотенцно.мстром, второй 2 - тахогенератором и третий W3 - дифференцирующим трансфор.матором, па вход которого поступает напряжение тахогенератора.

На рис. 10,7, б приведена структурная схе.ма рассматриваемого устройства. На ней обозначено: , - ко;)ффициспт передачи погенниометра, к-) - коэффициент не-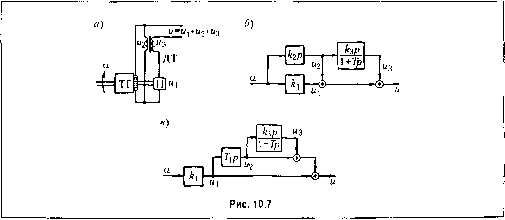

редачи тахогенератора, н Г -- коэф4)ици-ент передачи и постоянная времени дифференцирующего трансформатора.

Результирующая передаточная функция

\ + Тр

(10.20)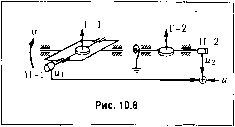

Структурная схема может быть приведена к виду, изображенному на рис. 10.7, в, ес;ш и выражеипи (10.20) вынести за скобки множитель ife,:

1+1\р+

\ + Тр

(10.21)

На рис. 10.8 приведен пример параллельного соединения гироскопических чувствительных элементов. Трехстепенный гироскоп V-1 сохраняет заданное положение в пространстве. Поэтому при наклоне основания иа выходе потенциометра Т\-1 будет возникать напряжение, нропорциональпое этому углу наклона: м, = ,а. Двухстеиен-ный гироскоп Г-2 работает в режиме датчика угловой скорости. При наклонах основания угол прецессии его можно приближенно считать пропорциональны.м скорости наклона. На выходе потенциометра П-2 будет поэтому напряжение kjja.CywwA напряжений и = u + и. определит резу.тьтирующую передаточную функцию

W{p) = ~ = k,+h,pk,{\ + Tp),

(10.22)

где T = -f-.

Этой передаточной функции соответствует структурная схема 10.6, а.

§ 10.4. Обратные СВЯЗИ

Как уже от.мечалось выше, обратные связи (см. рис. 10.1, в) могут быть положительными и отрицательными. Кроме того, обратные связи могут быть жестки.ш и гибкими. Для уяснения носледиего рассмотрим передаточную функцию (10.3), .записанную для случая отрицательной обратной связи. Из этого выражения найдем передаточную функцию для установившегося режима, для чего в (10.3) необходимо положить р = 0: