§ 17.4. Исследование систем с переменной структурой

Понятие о системах с переменной структурой было дано в главе 2, а об их уравнениях - в конце главы 16.

Покажем методику исследования систе.м с перемешгой структурой при отсутствии внешнего воздействия на примере системы второго порядка при линейном объекте и линейных структурах управляюп1его устройства, так что нелинейность системы будет заключаться в автоматическо.м переключении этих структур.

Имея в виду второй порядок системы, испо;п>зуем изображение процессов на фазовой, плоскости, которое для линейных систем нредставлепо было вьипе на рис. 16.8 -16.13.

Рассмотрим систему (рис. 17.20), пе обладающую при постоянной структуре собственной устойчивостью [32]. В самом деле, если = const, то уравнение системы будет

+ ckx = 0

и получатся незатухающие колебания, изображаемые на фазовой нлоскости концентрическими эллипсами (рис. 16.8).

Сгнели же звену придать вид, как иа рис. 16.27, где i переключением согласно фор.муле (16.71), где а = к, 3 = причем > > О, то получим уравнения системы

Y + kkx = Q при x,x>0, (17.93)

2 +k2kx = Q при xx<Q. (17.94)

Рис. 17.20

шинстве технических задач :-)того не получится. Однако видно, что описанный частотный критерий устойчивости В. М. Попова для систем с одной однозначной нелиией-ностыо в его графической форме может быть применен при любой сложности линейной части системы и численно заданных К(Х-)ффипиентах уравпепий. Более того, он может быть применен в случае, когда ие заданы уравнения, но известна экспериментально снятая амплитудпо-фазовая частотная характеристика линейной части W(j(a). Чтобы установить устойчивость системы согласно рис. 17.17, W(jia) надо перестроить в характеристику W* (/со), пользуясь формулами (17.85).

Очертание нелинейности может быть неизвестным. Необходимо лишь знать, в пределах какого угла (рис. 17.15) она расположена. Для конкретно задан1и>!х форм нелинейности область устойчивости, вообще говоря, будет несколько шире, по данным .методом это не определяется (см. гл. 18).

Первое из них будет действовать в первом и третьем квадрантах фазовой плоскости (рис. 17.21), а второе - в четвертом и втором квадрантах. С эллипса 1 в первом квадранте (соответствует коэффициенту k,) изображающая точка переходит на эллипс 2 в четвертом квадранте (соответствует коэффициенту ki), затем иа эллипс 3, копцспт-рический с первым (снова коэффициент ,), далее на эл-.П1ПС 4, концентрический с эллипсом 2, и т. д. В результате таких переключений система стаповится устойчивой.

В данном примере переходный процесс представляет собой затухающие колебания. В большинстве случаев для избежания колебательных процессов в системах с пере.меп-пой структурой следует стремиться реализовать скользящий режи.м. Для этого переключения в системе должны производиться в таких местах, где фазовые траектории направлены навстречу друг другу. Покажем это на примере. Пусть в той же систе.ме (рис. 17.20) звено также устроено по приинину рис. 16.27,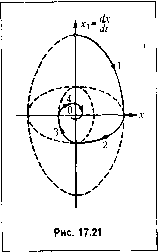

где,.-.

X] = - сх

Тогда прежнее выражение для Ц

[а при х,х>0, (3 при х,х<0.

получает другой смысл, Возьме.м при это.м Получим два уравнения системы:

Y + k,kx = Q при X\X>Q,

(17.95)

(17.96)

--([/a=0 при x,x<0.

(17.97)

Линиями ра,здела .между областями их действия будут

X = О и X, = г/ - сд: = О,

т. е, ось ординат и наклонная прямая па фазовой плоскости (рис. 17.22). При этом уравнение (17.96) будет действовать в первом и третьем секторах фазовой плоскости.

Поэтому там фазовыми траекториями будут служить согласно рис. 16.8 концентрические эллипсы. Уравнение же (17.97) будет действовать во втором и четвертом секторах фа.зовой плоскости (рис. 17.22), где фазовые траектории изобразятся в соответствии с рис. 16.3.

Обе эти линейные структуры (17.96) и (17.97) по отдельности не обладают устойчивостью. Б.!агодаря же переключениям систе.ма в цело.м становится ус-тойчнвой.

В отличие от нредыдун1ей системы, здесь, как видно из рис. 17.22, нет колебательного процесса. При любых начальных условиях фазовая траектория приходит на наклонную прямуюх, = О, где она встречается с фазовой траекторией

с противоположным ей направлением движения. По.этому переход и.зображающсй точки через нря.мую х, = О невозможен. В результате изображающая точка вынуждена двигаться вдоль прямой х, = О в сторону начала координат, что и представляет собой скользяишй режи.м переходного процесса в данной системе.

Практически скользящее движение будет сопровождаться вибрациями вследствие быстрых переключепий то в одну, то в другую сторону, как н показано на рис. 17.22. Ввиду неидеальпостн системы (дополнительной инерционности или зана.здываюгя) эти вибрации будут иметь конечные амплитуду и частоту При идеально.м же рассмотрении, цроведенно.м выше, амплитуда их равна нулю, а частота - бесконечности.

Рассмотрение реатьпого переходного процесса скользящего типа с конечными вибрациями за счет дополнительной инерционности, повышающей порядок уравнения, возможно с по.моп1Ью приближенного .метода гармонической линеаризации. Это можно сдедать аналогично рассмотрению .\гедленно меняющихся сигналов в автоколебательных системах (§ 19.2), если за медленно .меняющийся сигнал принять осиовиос апериодическое движение в скользящем н])оцессе, а наложенные на пего вибрации рассчитать, как автоколебате.тьпую составляющую процесса (см. [73]).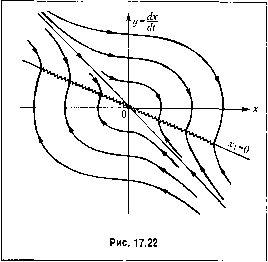

Глава 18 ,

ПРИБЛИЖЕННЫЕ МЕТОДЫ ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ И АВТОКОЛЕБАНИЙ

§ 18.1. Гармоническая линеаризация нелинейностей

в .этой главе будет изложен метод гармонической линеаризации для приближенного определения периодических решений (автоколебаний) и устойчивости нелинейных систем любого порядка, который но идее близок к методу эквивалентной линеа-