Идеальная релейная характеристика. Для идеальной релейной характеристики (рис. 19.6,6), полагая в последних формулах 6 = 0, получи.м

2с . ж F = - arcsm -

4с q= - тиг

(19.79)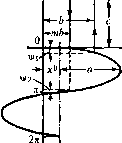

f (xo-tasiimi)

п п 3 271 v=a)t 2 2

arcsm 2=. arcsin

Рис. 19.11

ири a > I дг [.

Релейная несимметричная характеристика. Релейная несимметричная характеристика при гармоническом и.зменении входной величины д:со смещенным цептро.м колебаний представлеиа на рис 19.11, а. Так будет изменяться напряжение на потребителе, управ.ляемом реле, если реле при срабатывании включает потребитель на полное напряжение, а при отпускании вглключает.

Вычисляя постоянную составляющую но формуле (19.6), получим

f lF(x4asinv/)i/v/ = --(n-Vs-vj/,).

После подстановки значений соответствующих углов имеем

2 2л

. Ь-х . тЬ-х arcsi н-+ arcsi н-

(19.80)

при а>\Ь-х\ Далее

а> \х -тЬ .

q = - \F{x +asin\;)cosv/rfy =-(cosy, -cos\i;2) Tta ТШ

или, с учетом значений углов xi/j и \)/2,

.0\2

(mb-x )

(19.81)

при а

Ь-х° и а>\х-7пЬ\.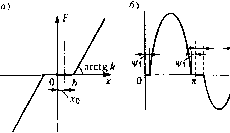

.V2 4/2

h-rO . h+rO

yi = arcsm Д , 412= arcsm-

Рис. 19.12

Наконец,

9 = - f/X-i +a.sim)/)cos\)/(fw =

ТТЛ j

= -(sini)/2-sin\)/,)

или, с учетом соответствующих синусов,

д = -(1-т) (19.82)

при тех же ограничениях.

Нелинейная характеристика с зоной нечувствительности. Нелинейная характеристика с .чоной нечувствительности изображена на рис. 19.12, а. Коэффициент q в этом случае равен нулю, так как характеристика однозначная.

Определим значения постоянной составляющей F (а, х ) и коэффициента гармонической линеаризации q (а, .г ) в соответствии с видом функции f (х + а sin показанной на рис, 19.12,6.

Для постоянной составляющей имеем

F=~\F(x+asm\v)d\ii = 2л

[asinv/-(6-x)J/v/- I k\asin\\-{b + x)]d\f

= -(COSVjr, -C0SV/.2) + ALr +-[ft(v(r, -V/2)-.r(\/,

что после подстаьювки соответствующих углов дает

+ kx +

+- л

arcsin-

. h-x

--arcsin-

, b + x

. ft-x . ft + x arcsi n-+ arcsi n-

(19.83)

приа> fe + x°.

Вычисляя коэффициент q получаем

J 2п

q = -- 1 -l-flsinv/)sinv/(iw =

1 . .

K-(v/] +V(r2)+-(sin2v(ri +sin2\/2)

- -[(6-x)C0SV/i +(Ь + х)С051(Г2],

что с учетом значении углов дает

q = k--

arcsin-+ arcsin --- +

а V

1 (*z£!)!+i±£! 2 V

(19.84)

при а> b + \x\.

Нелинейная характеристика с насыщением. Для нелинейной характеристики с иасыщеиием (рис. 19.8) при несимметричных колебаниях аналогичным путем получаем следующие значения постоянной составляющей F {а,х) и коэффициента гар.монической линеари.зации q {а, х );

.0\2

(6 + х )

.0ч2

(6-х )

+ (6+х )arcsin-+(6-х )arc.sin-

. 6-х . б + .г

arcsm-+ arcsi n-+

6-х I (6-л- ) Z+x I (б + х )

.0 ч2

(19.85)

при а > 6 + х .

Проиллюстрируем на нриме1)е данной нелинейной характеристики графики

= /l

, 6 ,

ири разных

:х - = con.st и т = /2

при разных = const, вычисленные

по формулам (19.85) и представленные иарис. 19.1.3.