В cooTBCTCTBiHi с, расчетом, нродела1гным вьппе, для л. а. х., изображенной па рис. 12.11 и рнс. 14.11, получаем требуемое значение постоянной времени

М-\ 12,2Vl,5--l

= 0,142 с.

Частота среза л. а. х.

(0, = Кх, =ioJ-J = 12,2J- = 21.2 с-.

1,5-1

to :\ i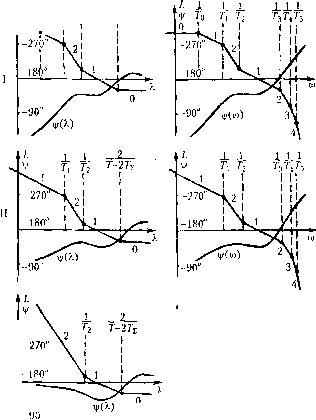

В соответствии с фо].)му;011 (15.41) ио.лучаем далее

2 М + 1 21,2 1,5 + 1

откзДа допустимый период дискретности Г< 0,0568 с. В случае учета постоянных времени Г 72 и н.меем

---(Г, +Т, +70 = 0,0284-0,013 = 0,0154 с 2 т,р М + 1 -

и допустимый период дискретности 7 < 0,0308 с.

Лиалогичшяе расчеты для случая М = 1,2 дают Tj - 0,2 с, со = 30 с и Г< 0,0368 с (ири Г, = Т, - Гз = 0) и Т< 0,026 с (прн ф О, Г2 О и Г3 0).

На рис. 15.9, б для иллюстрации построены переходные процессы при воздействии па входе в виде едипичиой ступенчатой функции. Переходные процессы построены посредством разложения вряд Лорана г-преобразования выходной величины.

Таким образом, С1ттез следящих систем методо.м л. а. х. на основе частотных критериев качества (по точности и запасу устойчивости) оказывается применимым и для систе.м, содержащих в своем контуре ЦВМ. При этом все расчеты сохраняют свою простоту и наглядность.

Для расчета удобно применять абсолютную псевдочастоту, которая в области низких частот (левее частоты среза) совпадает с обычной угловой частотой ш. При этом в области высоких частот л. а. х. приход1ГГся строить по сумме мшп>х постоянных времени. Влияние кваитоваиия ио времени, вносимое ЦВМ, легко учитывается нрн гюстро-ении только л. а. х., без необходи.мости расс\готреиия фазовой характеристики.

Для облегчения процесса синтеза можно ввести поиятие типовых л. а. х. систем управления с ЦВМ. На рис. 15.10, й приведены типовые л. а. х. для статической систс-мГ) п астатической первого и второго порядков без учета временного запаз/и)1вания. На рис. 15.10, б изображены соответствующие им л. а. х. непрерывной части, а в табл. 15.2 приведены передаточные функции.

Синтез непрерывных корректирующих средств. В импульсных системах (глава 14) .иш коррекции используются иепрерьпщые корректируюпцте средства. Наиболее просто производится расчет корректирующих средств последовательного типа. В это.м случае дпскреттшя передаточная функция разомкнутой системы должна равняться желаемой передаточной (})упкцпи

WJ,2)=W,Mz). (15.55)

Здесь U/, ;U/o(2) представляет собой дискретную передаточную функцию последовательно включенных корректирующего звена с передаточной функцией VF k(p) и непрерывной части с нередаточной функцией Wq(p). Напомним, что W iWq{2) VV, ;(2) Wq(z). Поэтому расчет последовательных корректирующих средств в дискретных систе.мах не является столь простой задачей, как в непрерывных системах.

Таблица 15.2. Типовые передаточные функции

Тип л. а. X

Степень астатнз ма

Дискретная частотная передаточная функция

Передаточная функция непрерывной части

К{\+]ХТ2)

(\ + jkT,)(i+j\7\) \+jk

X \ +jX

K{l + T.,p)x

x{(\ + T,p)(\ + T,p)x х(1 + Гзр)...(1 + Г;р)...}-

K(\+T.,p)x

х{/(1 + 7;р)(1 + ГзР)х x(l+7 ...(l + 7:p>..}

V J

(jXf l + jX

K{l + T.,p)x

x{p\\ + T,p){\+l\p)...

...(\+Tp)...}-

1 + 7 ~-T

T=Y,Ti-h+r,+...+

Однако выше было показано, что л. а. х. дискретных систем, построенные в функ-

2 (л)Т

НИИ абсолютной псевдочастоты X = -tg-y- для частот X < 2/Г практически сливаются с л. а. X. непрерывной части. Поэто.му можно воспользоваться известными приемами расчета последовательных корректирующих средств, если в качестве желаемых л. а. X. использовать характеристики, соответствуюпп1е передаточным фу1Н<циям непрерывной части.

Требуемый вид последовательного корректирующего звена определяется в это.м случае по виду л. а. х., полученной вычитанием ординат л. а. х. нескорректированной системы из ординат желаемой (типовой) л. а. х.

Рассмотри.м иллюстративный пример [9].

Пример. Произведем расчет системы с астатизмо.м первого порядка по следующим исходным даипы.м: максимальная скорость слежения Q, ax = 20 град/с; максималь-