а) q

Рис. 18.6

дне/, входяидис в уравнение (18.34), сложно зависят от а.мнлитзды я, а в ряде случаев и от частоты со. В таких случаях удобнее указанное уравнение загтсывать в виде

Q(jm) + R<Jm)(q +jq) = 0.

(18.39)

не подставляя зависи.мости q и q от я и со. Тогда в.место уравнений (18.36) получим для определения периодического решения уравнения:

Х(со,, </) = 0, Y(m,q,q) = 0.

(18.40)

Для обидего случая задач, в которых каждый из ко-эс})фициентов гармонической ;шнеаризации / и q зависит сложным образом от обеих неизвестных я и со, т. е.

= f/ (я, 0)), с/ = q (а, со),

(18.41)

можно применить следуюндии прием решения.

Задаваясь различными значениями я и со, построим по ({юрмулам (18,41) две серии кривых: (со) н q (со) при разных я = const (рис. 18.6). Зате.м из уравнений (18.40) выразим

= Z, (со), q = Z2 (со)

(18.42)

и эти две кривые нанесем на тех же графиках. Теперь остается на этих двух кривых найти такие точки С и В, в которых кривые Z, (со) и Z2 (со) пересекают линии с одинаковыми зиачения.ми я ири одном и то.м же значении со. Полученные величины я и со будут решением задачи, т. е. амплитудой я и частотой со искомого периодического решения.

Во многих встречающихся иа практике задачах вместо (18.41) будет

q = q(a) и q=q(a).

(18.43)

Тогда кривые q и q иа рис. 18.6 для разных амплитуд будут и.меть вид горизонтальных прямых ли1И-1Й.

В простейп1ем случае, когда в системе имеется однозначная нечетно-симметричная иелинейпость F (х), для которой q = q (а) и 7 = О, из уравпени11 (18,40) можно найти

(?(я) = г(со), (18,44)

Тогда, исключив q из уравнений (18,40), найдем частоту со = со как функцию параметров системы. Затем, изобразив график зависимости q (я) (рис, 18.7), проведем на нем согласно (18.44) горизонтальные линии q = Z(co) для разных постоянных зиачеиий со = со , т. е, для разных соотиошепий параметров chctc.vhjI. Точки пересечения этих

прямых ((О = (0 ) с кривой q (а) (например, на рис. 18.7 точки а , и а 2) определяют в каждом случае амплитуды периодических ренгений. Если пересечений нет, то и периодических penieinm в системе не будет. В простейших случаях уравнение (18.44) репгается анатнТ1[чески.

Графический способ. Для гармонически линеаризованного характеристического уравнения (18.33) можно 1шписать выражение кривой Михайлова [73]

D(j(b) = Q{j(h)+R(j&)

, q(a,(o)

X(Q)

0 e ! a ! Рис. 18.7

(18.45)

где знак - введен, чтобы отличать текущий пара.метр б), изменяющийся вдоль кривой Михайлова, от частоты (о, входян[ей в выражение гармонической линеаризаиии нелинейпости.

Исколгое периодическое решение х, = а sin О) ?, т. е. неизвестные а и (о определятся прохождением кривой Михайлова через пачагю координат (рис. 18.8, а). Поскольку в точке [грохождения кривой Михайлова через начато координат текуп1ее зпаче1П1е ш должно совпадать со значением 0) = (о , входящим в коэс})фициенты гар.монической линеаризации, то для удобства решения можно заранее отождествить в выражении (18.45) значения й и со. Тогда иско.мые частоту со = (0 и амплитуду а = а автоколебаний .можно будет определить путем построения кривых

f{(a) = Q(j(a) + R(jm) [q{a,со) +jq{а,(о)] = О,

(18.46)

которые в общем случае пе будут совпадать с кривы.ми Михайлова. При это.м надо выбрать такое значение а, при которолг кривая пройдет через начало координат.

Если, например, для каких-нибудь трех различных значений а кривые/((о) проходят у ка.заниы.м иа рис. 18.8, бобра.зо.м, то искомые значения а = а и 0) = (о можно найти путем следующей интерполяции:

АО, , СО.

:( :;- 2). = Щ+7(<Ъ-Щ)-

АВ

Этот способ целесообразегг лишь в самых сложных случаях, когда и:адожеицые выше способы не удается при.меиить.

Использование коэффициентных соотношений для определения периодического решения. Для обнаружения ({)акта наличия пары чисто мнимых корней в характеристическом уравнении (18.33) можно также применить известные алгебраические критерии устойчи-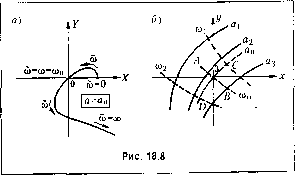

вости линейных систем. Так, если гармонически линеаризоваг1ное уравнение (18.3,3) нелинейной системы имеет третью степень относительно р, то его можно записать в виде

ор + ip2 + а2Р ~ 3 = О, (18.47)

причем коэффицие1[ты его будут содержать в себе иско.мые значения частоты со и амп;и1туды а, автоколебаний.

Условие наличия нары чисто .мнимых корней по критерию Гурвгищ (см. § 6.2) будет

aia2 =ao 3- (18.48)

Оно дает только одно уравпение с двумя неизвестными а и со . Чтобы найти второе, представим уравнение (18.47) при наличии мнимых корней р ± jco в виде

(Р + )(аоР + Ь) = 0.

Раскрыв здесь скобки и приравняв коэф(})ициенты этого уравнения соогветствую-щи.м коэ(}х})ицие1Ггам (18.47), найде.м

Яоп = 2- (18.49)

Из двух уравнений (18.48) и (18.49) определяются неизвестные амплитуда я и частота со автоколебаний, входящие в состав коэ(}х})иииентов (18.47). При это.м точш) также, как в основном способе, здесь на основании уравнипш (18.48) и (18.49) можно строить графики зависимостей я и со от одного параметра системы или на плоскости двух параметров с целью их выбора.

Если гармонически лииеаризоваи1юеуравпение (18.33) нели11СЙ1юй системы имеет четвертую степень отпосительнор:

Яор* я,р + a-ip -1- a.j) + Я/, - О, (18.50)

то углювие наличия пары чисто мнимых корней согласно § 6.2 будет

Яз(я1Я2 - ЯцЯз) - Я/, я =0. (18.51)

Кроме того, записывая уравнепие (18.50) в виде

(р2 + а)2) (я,2 + ip = 0

раскрывая здесь скобки и приравнивая полученные коэффициенты соответствующим коэ(})фициента.\1 (18.50), находп.м

я.сояз. (18.52)

С иомо1цьюдвухуравпеиий (18.51) и (18.52) решаются все вышеуказанные задачи для пелипейпой системы четвертого порядка.