воздействиям (задающему и возмущающему), которое применяется в комбинированных системах.

Здесь мы рассмотрим только линейные алгоритмы, когда управляющее устройство вырабатывает величину м(0 в функции отклонения, или ошибки х{1) в соответствии с линейной формой

u{t) - кх + к2Х + к-х+ ... + к \xdl + 5 \\xdf+ ....

1. Пропорциональное управление. В случае пропорциоца.1Ьного управления ал горитм уп1)авле1Шя имеет вид

U(t) = k\X{t) .

11есмотря па простоту, такой а,пго1)Пт.м исполызуется во многих системах автоматического управления, в том числе и в тех, схемы которых и;юбраже1нл на рис. 1.11-1.16. Однако в ряде случаев при его при.мспснии желаемое качество процессов в систе.ме не может быть обеспечено. Это объясняется те.м, что нропорциональпое управление действуют слпщко.м прямолинейно : есть отклоните - есть управление (рис. 2.7, а). Из-за инерционности элементов управляющего устройства (усилителей, исполнительных устройств и др.) управляющее воздействие в своем изменении будет запа.здывать по отношению к изменению ошибки (пунктирная кривая на рис. 2.7, а). Поэтому в момент времени fj, когда ошибка становится равной нулю, управляюп1ее воздействие будет продолжать действовать в прежнем направлении, в1,П1ужлая ее вновь увеличиваться, и;!.\енив знак. В результате процесс в системе .может стать слишком колебатсльпы.м и даже расходяпи1Мся.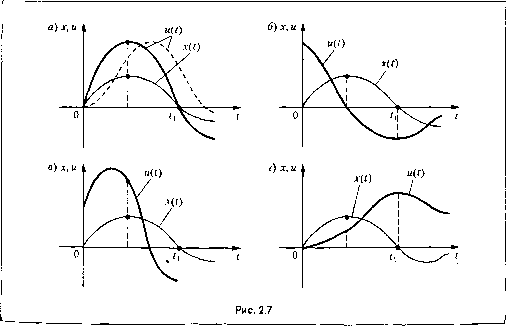

2. Управление по производным. При управлении по первой производной от ошибки осуществляется зависимость

т. е. унравляюпее устройство реагирует не на саму ошибку, а на скорость ее изменения (рис. 2.7, б), и поэтому действует с унреждение.м, стремясь не допустить появления ошибки.

Управ;1ение по производной не имеет самостоятельного значения, так как в установившемся состоянии, когда опгибка постоянна, производная от ошибки равна нулю и управление П1)скращается. Однако оно может играть весьма большую роль в переходных процессах и вообще в динамике в качестве вспомогательного средства, так как такое уп])авлепие позволяет учитывать не только наличие ошибки, но и тенденцию к росту или уменьшению ошибки. Поэтому управление по производной обычно сочетается с управлением по отклонению:

u(0-kix(t) + k2x(t).

При использовании такого алгорит.ма управляющее воздействие возникает даже

в том случае, когда л: = О, но х 0 (рис. 2.7, в), и существует до тех пор, пока x?t 0. Кроме того, оно изменяет свой знак раньше, че.м сама ошибка, т. е. действует с упреждением. В результате введения управления но производной от ошибки увеличивает скорость реакции систе.мы управления, повышает ее быстродействие, что приводит к снижению опптбок в динамике.

В некоторых случаях в алгоритм управления .могут вводиться производные более высоких порядков - вторая, третья и т. д. Это еще больше улучшает динамические качества chctcmfj автоматического управления. Однако в настоящее время техническая реализация производных выше второго порядка встречает значительные трудности.

3. Интегральное управление. При интегральном управлении осуществляется пропорциональная зависимость между скоростью изменения управляющего-воздействия и ошибкой:

й (t) = k.iX(t).

При это.м управляющее воздействие получается 11{?опо)ци9нальиым инте1ралу от ошибки по времени:

и (t) = k- x{t)dt.

Этому алгоритму присуще важное и полезное для практики свойство, состоящее в том, что после окончания переходного процесса при x{t) = О управляющее воздействие может сохраняться (рис. 2.7, г). Это свойство широко используется для повышения точности автоматических систем. Однако вместе с тем применение интегрального управления делает систему более замедленной в действии, т. е. снижает ее быстродействие, а также приводит к ухудшению устойчивости (последнее будет показано ниже в главе, посвящетюй устойчивости). Это объясняется те.м (рис. 2.7, г), что величина интеграла в некоторый момент вре.мени пропорционапьпа соответствующей

площади под кривой х(с). Поэтому при возникновении ошибки управляющее воздействие накапливается постепенно, запаздывая по отиощснию к изменению оп1иб-ки.

Управление с целью повыщепия точности системы может осуществляться и по второму интегралу от ошибки по времени:

u(t) = k3llx(t)dtdt.

Однако при этом снижение быстродействия станет еще более заметным. 4. Изодромное управление. При изодромно.м управлении осуществляется зависимость

u(t) = kxit) + \x{t)dt.

Такое управление сочетает в себе высокую точность интегрального управления с большим быстродействием пропорционального управления. В первые моме1ггы вре-.мепи при появлении ошибки система изодромпого управления работает как система пропорционального управления. Это определяется первым слагаемым в правой части алгоритма управления. В дальнейшем система начинает работать как система интегрального управления, так как с течением времени преобладающее значение начинает приобретать второе слагаемое

В общем случае алгоритм управления может иметь сложный вид и содержать кроме члена, пропорционального ошибке, также интегралы (для улучшения точности) и производные (для улуЧ1пе11ия динамических свойств) от ошибки. Так, например, часто используется изодромное управление с введешем первой производной

u(t) = x(t) + k2X (О 4- 3 jx{t)dt.

Для линейных алгоритмов управления детально разработаны многочисленные прикладные методы исследования (анализа и синтеза), различные расчетные и экспериментальные приемы определения устойчивости, точности и качества процесса управления, а также схемы конкретных технических устройств формирования линейных алгоритмов.

§ 2.3. Нелинейные алгоритмы управления

Использование нелинейных алго]жтмов управления, определяемых разнообразными иелинейпыми уравнениями управляющего устройства

f,(м, du/dt,...) = Fix, dx/dt,и, /, g),

значительно расширяет возможности целесообразного изменения качества процессов управления. Это ясно из обп[ИХ принципиальных соображений, так как область нелинейных уравнений значительно богаче и разнообразнее, чем линейных.

Несмотря на то, что общей теории нелинейных алгоритмов нет, исследования и опыт применения отдельных частных видов этих алгоритмов говорят об их большой практической эффективности. Отсюда следует актуальность их теоретического изучения.