и для ошибки

Выражение

называется передаточной функцией замкнутой системы. Она устанавливает связь между управляемой величиной и задающим воздействием при равенстве нулю возмущающих воздействий:

Выражение

yit)Ф(p)g(t) = Jg{t). (5.21)

называют передаточной функцией замкнутой системы по ошибке. Оно дает связь между ошибкой и задающим воздействием в замкнутой системе при равенстве нулю возмущающих воздействий:

х(0 = Ф.(;)ё(0-у. (5.23)

Как и ранее, формулы (5.18), (5.19), (5.21) и (5.23) представляют собой символическую (операторную) .запись дифференциальных уравнений. Более строго передаточную функцию замкнутой системы можно определить как отношение изобра-. жений управляемой величищ)! У(р) и задающего воздействия G{p) при нулевых начальных условиях и отсутствии внешних возмущений:

а передаточную функцию но ошибке - как отношение изображений ошибки Х(р) и управляющего во.здействия G(p):

также при нулевых начальных условиях и отсутствии виепших возмущений.

Из формул (5.18) и (5.19) видно, что введение автоматического управления уменьшает отклонение управляемой величины под действием воз.мущающих воз-

действий в [1 + UO?)] раз по сравнению с отклонением в разомкнутой системе (5.12). когда цепь управления разорвана и автоматическое управление отсутствует.

В результате сравнения 4)ор.мул (5.4), (5.20) и (5.22) видно, что характеристический иолипо.м за.мкнутой систе.мы D{p) представляет собой по;1ином знаменателя передаточной функции замкнутой систе.мы:

D(p)-B(p) + C(p). (5.24)

Он равен сум.ме полиномов числителя и знаменателя передаточной функции разомкнутой систе.мы (5.13).

Приравнивание нулю характеристического полинома (5.2А) д,астхарактеристи-уеское уравнение замкнутой системы:

Dip) = Bip) + Cij>) = 0.

Оно может быть записано в более удобной ({)ор.ме, которая непосредственгю получается из (5.18) или (5.19):

1 + Wip) = О, (5.25)

Полином знаменателя передаточной функции ра;юмкнутой систе.мы Cip) представляет собой характеристический полином разо.мкнутой систе.мы.

M;i рассмотренного видно, что знание передаточной функции ра;!0.мкиутой системы позволяет найти вы1)ажение для оитбки и управляемой величины в функции задающего и возмущающих воздействий, а также характеристическое уравнение систе.мы.

Передаточная функция разомкнутой системы может находиться неносредственио по структурной схеме и передаточным функциям входяпп1х в нее звеньев (см. ниже, § 5.3).

§ 5.3. Использование структурных схем

Составление основных уравнений системы авто.матического управления (5.18) и (5.19) во многих случаях .может быть значительно облегчено использованием понятия дина.мических зве1Н>ев. Динамические звенья были подробно рассмотрены в главе 4. Часто систему автоматического управления можно рассматривать как комбинацию динамических звеньев с оиределенными типовыми или не тиновы.ми пере-даточиы.мн функциями. Изображение системы регулирования в виде совокупности дииа.мпческих звеньев с указанием связей между ними носит название структурной схемы. Структурная схема .может быть составлена па основе известных уравнений системы, и, наоборот, уравнения системы могут быть получены из структурной схемы. Однако первая задача может иметь различные варианты решения (различные структурные схемы), тогда как вторая задача имеет всегда едипствегиюе регпение.

Элементы структурных схем приведены в табл. .5.1.

PaccMOTpn.vi вначале простейшие сочетания звеньев.

Последовательное соединение звеньев. Такое соединение показано на рис. 5.2.

Таблица 5.1

Наименование

Звено с одним входом

Звено с двумя входами

Узел (разветвление)

Обозначение

Наименование

Сумматор

Элемент сравнения (для отрицательных обратных связей)

Обозначение

хз - д:, - Х2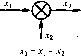

Нетрудно показать, что результирующая передаточная функция равна произведению передаточных функций отдельных звеньев:

W {p) = W,{p) Wip) W.,{p), В,Хр) В,(р)В2(р)В(р)

Cpip) С,(р)С2(р)Сз(р)

(5.26)

(5.27)

Следует подчеркнуть, что это справедливо только в том случае, если соединение выхода предыдущего звена со входом носледуюп1его не меняет исходныхуравиений каждого звена и, следовательно, его передаточной функции. В подобной последовательной цепи звеньев сигнал проходит только в одном направлении.

Если при соединении двух звеньев наблюдается влияние одного звена иа другое, в результате чего .меняются исходгнье уравнения какого-либо звена, то такое соединение двух звеньев должно рассматриваться как повое са.мостоятельгюе звено со своей передаточной функцией.

Параллельное соединение звеньев. Такое соединение звеньев изображено на рис, 5.3.

Так как сигналы на выходе всех звеньев складываются, то результирующая иере-даточная функция равна сумме передаточных функций:

W ip) = W,(p) + W2(p) + W,ip) =

В,(р) В2{р) , В.,{р)

С,(р) C.j,(p) С.,{р)

(5.28)

Здесь остаются справедливы.ми замечания, сделанные вьнпе относительно вза-и.много влия>шя звеньев.