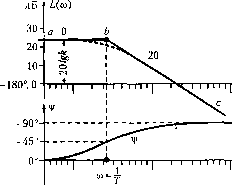Рис. 4.12

Наиболее просто, практически бе,з вычислительной работы, строится так называемая асимптотическая л. а. x. Ее построение показано иа рис. 4.12. На стандартной сетке проводится вертикальная прямая через точку с частотой, называемой сопрягающей частотой со = 1 /7. Для частот меньнн1х, чем сопрягающая, т. е. при со < 1/Г, можно пренебречь вторым слагае.мым иод корнем в выражении (4.24). Тогда левее сопрягающей частоты (рис. 4.12) .можно заменить (4.24) приближеи-пым выражением 1(со) = 20 lg/г (при о) < 1/Т), которо.му соответствует пря.мая линия, параллельная оси; частот (пря.мая аЬ) и являюиаяся первой асимптотой.

Для частот больн1Их, чем сопрягающая (со > 1 /7) в выражении (4.24) .можно пренебречь под Kopite.M единицей по сравнению с (j}T~. Тогда вместо (4.24) будем иметь приближенное значение

L((o)=:20lg- (при со > 1/7),

которому соответствует, согласно § 4.4, прямая с отрицательным iiaiuionoM -20 дБ/дек (прямая be), являющаяся второй асимптотой.

Ломаная линия аЬс и называется асимптотической л. а. х. Действительная л. а. х. (показана па рис. 4.12 путсгиром) будет несколько отличаться от аси.мптотической, причем панбольиюе отю-юнение будет в точке Ь. Оно равно приблизительно 3 дБ, так как

= 20lg- = 201g-3,03 дБ, V2

что в линейном масштабе соответствует отклонению в л/2 раз. На всем остальном протяжении влево и вправо от сопрягающей частоты действительная л. а. х. будет отличаться от асимптотической менее чем на 3 дБ. Поэтому во многих практических расчетах достаточно ограничиться построением асимптотической л. а. х. На том же рис. 4.12 показана логари(}5мическая фазовая характеристика. Характерными ее осо-бетюстями являются сдвиг но фазе \/ = -4,5° на сопрягающей частоте (так как arctg 0)7= arctg 1 = 45°) и сим.метрия л. ф. х. относительно сопрягающей частоты.

3. Апериодическое звено второго порядка. Дифференциальное урав1[енне звена имеет вид

(4.25)

t- Г4Г.<Г. t-> -\

ii = const

. -г г) R. R,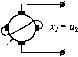

\-U-L

Х2-Р2

X2~l

X,= 0-

C,X C2

X2=U2

Рис. 4.13

При этом корпи характеристического уравнения Т2р + Тр +1=0 должны быть веществе)шы,ми, что будет выполняться при условии Г, > 2Т2. В операторной записи уравнение (4.25) приобретает вид

(Т2Р2+Т,р+\)Х2 = кх,.

Левая часть последнего выражения разбивается па множители:

(T:iP+\)(T+\)x2-kx

(4.26)

(4.27)

Передаточная функция звена

Щр)=-

Апериодическое звено второго порядка эквива-тентно двум апериодическим зве-нья.м первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи к и постоянными времени Т ., и .

Примеры апериодических звеньев второго порядка приведены на рис. 4.13. Рассмотрим подробно случай двигателя постоянного тока (рис. 4.13, а). При отсутствии момента нагру.зки на валу и при учете переходных процессов в цепи якоря динамика Двигателя описывается дву.мя уравиеиия.\И1, определяющи.ми равновесие э. д. с. в цени якоря:

L + Ri+CpQ = u, dt

и равновесие моментов на валу двигателя:

Левее первой сопрягающей частоты (со < 1/7з), это выражение заменяется приближенным

1(со) 20 Ig k,

кото]юму соответствует прямая с пулевы.м наклоном (первая асимптота л. а. х.). Для 1 1.

частот J, выражение (4.30) заменяется нриближепны.м

1(ш) = 20 Ig к/ш1\ ,

которому соответствует прямая с отрицательным [[аклоном -20 дБ/дек (вторая асимптота). Для частот со > выражение (4.30) заменяется нриближепны.м

1(со) = 20 Ig к/ю%Т.

которо.му соответствует прямая с отрнцате;(ьным наклоном -40 дБ/дек (третья асимптота). Действительная л. а. х. показана в табл. 4.3 пунктиром. Она отличается от асимптотической в точках излома на 3 дБ,

где и - напряжение, прикладываемое к якорю, и С\ - коэффициенты нропорци-опалыюсти между обратной э. д. с. и скоростью вращения Q и между вращающим моментом и током якоря i,J ~ приведенный момент инерции, /. и R - индуктивность и сопротивлениеiwim якоря.

Переходя в обоих урав}1ениях к операторной фо[)ме записи и рещая их сов.местпо, получим передаточную функцию двигателя постоянного тока при управлении напряжением якоря как отнощепие изображений скоЮСти двигателя и напряжения якоря:

{Р) = ~--. ... 2 (4.29)

где 7] = = J----электромеханическая постоянная времени двигателя,

7 = R/L - электро.магиитпая постоянная времени якорной цен1[, Qq и Л/ц - скорость холостого хода и пусковой момент двигателя.

Для того чтобы корни знаменателя выражения (4.29) были вещественными и передаточную фут<цию можно было бы представить в форме (4.28), необходн.мо выполнение условия 4Гя 7;,.

Переходная функция и функция веса звена приведены в табл. 4.2.

Частотные характеристики приведены в табл. 4.3. Построение асимптотической л. а. x. производится аналогично то.му, как это было сде.чапо для апериодического звена первого порядка. Вначале проводятся вспомогательные вертикальные линии через сопрягающие частоты со = 1 /TJ, и со = \/Т/.

Для определенности цост1)оепня принято, что T-j > Т/.

Л. а. x. строится по выражению

L(co) = 201giy(7CO) = 20lg Д о..