д = ~л1(1 -Ь, q =-

(18.110)

При этом из (18.102) находим

(1 + г,У,)(1+7>;:)

(in =

(18.111)

а пз (18.103)

7tfxBi,(l+7;4.)(l+7(.f,)

/4(1-7] т; of,)

(18.112)

По этим (})ормулам ностроет ! кривые на рис. 18.21, о и г, определяющие амплитуду и частоту периодического решения в :!авпси.\1ости от величины параметра k. Устойчивость пе])ИОДНческого решения определим здесь ио методу осреднения периодических коэффициентов. Для вычисления коэффициента х{а) согласно (18.60) нужно знать производную от и пох, которая, однако, обращается в бесконечность нрих = Ь, когда рх > О, и нрих = = -ft, ко)да рх<0. Чтобы избежать ;этого,.заменим -заданную характеристику (рис. 18.20, г) 1говой (рис. 18.22, а), из которой заданная получается предельным переходом (другой способ, с дельта-функцией, см. в § 18.5, рис. 18.37). Для характеристики па рис. 18.22, а при изменении величины

6) X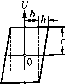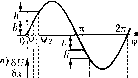

(at

(7l+Vl)(7C+V2)2n

Рис, 18.22

изображенная на рис. 18.21, б. Здесь во.зможен только автоколебательный процесс; область устойчивости равновесного состояния, имевшаяся па рис. 18.21, а, пропадает.

Как видим, зона нечувствительности имеет стабилизирующее значите для ре-.тейкой системы, приче.м цнфина области устойчивости (О < < k согласно (18.108) пропорциопальна цщрине.зоны нечувствительности 2й. Сравнение данного решения, учитьшаюгцего инерционность Г, срешением без учета 1\ показывает прииципиаль-иую важ1Ц)сть учета этого фактора. Например, для характеристики вида рис. 18.20, в без учета 7;j получится только устойчивость (а = 0) при .чюбых числовых значениях пара.метров (что нереально), а с учетом T-j - только автоколебания (рис. 18.21, б). Для характеристики вида рис. 18.20, б вместо неограпичетгой области устойчивости (без учета 7з) получается ограниченная и возникает енге область автоколебаний с большой амплитудой при одновременном существовании устойчивости в .малом (рис. 18.21, а).

Далее, в третьем час гном случае, когда характеристика реле чисто гисте[)езисная (рис. 18.20, г), т. е. й, = -Ь. = -Ь, из (18.99) имеем

X по закону-г= а sin cot (рис. 18.22, б) производная принимает значеиня, показан-

1ыепарис. 18.22, в, где

VI/, =:arcsin-, V1/2 = arcsin (18.113)

Осреднетюе ее значение (18.60) согласно рис. 18.22, в с предельны.м переходом к заданной характеристике {h 0) будет

2fH>2-¥.) 2с;(у2-¥,)

Х{а) = \тл- -= lim -.-,

Л->о 271 VjVi Jta(sinv/2-.sinv/i)

так как /г = а sin V2 ~ -п Vi-

Обозначив \/2 \/, А\/ и взяв производные от числителя и знаменателя по Л\/, получим

/ ч 1- 2с 2с

a4->0 7iacos(v/,+А\;) Tiyja--Ь (18.114)

Итак, для исследования устойчивости получаем следующее характеристическое уравнепие:

Г, T.g? + (Г, + 7з) p+p + k,kx{a)-0. (18.115)

Условие устойчивости периодического решшя, следовательно, по критерию Гурвица будет

{Т,+ Т.)>1\Т;кфХ{а).

Подставив сюда >(г(а) из (18.114) и значения и из (18.111) и (18.112), убедимся, что оно выполняется. Следовательно, в системе будут автоколебания X = a,jsin сОд а.мнлитуда и частота которых определяются графиками рис. 18.21, е и г или с!)ормулами (18.111), (18.112).

Пример 6. Пусть в той же системе характеристика реле имеет простейпгий вид рис. 18.20, о, но имеется постоя шюе но времени запаздывание т. Тогда согласно (18.1 Ю), где 6 = 0, уращ1ение нелинейного звена будет

t/ = ie- x.

71(2

В результате получим характеристическое уравшчше системы {T,p + \){T,p-\)p + k,k~e-x = 0.

Подстановкар = ум с учетом выражения с = cos тсо jsinico даст два уравнения:

Х = -costco-(7, +T:j)co =0, па

Y = -sium + oi-TTu? =0,

из которых находим два соотноиюиия:

(7 , + 75 )со tgiM = 1 - ГTwl,

=

Аскк

nbiJ\ + (T,+T!)(iyl+T;Tia,l

Первое из них определяет частоту (решается графически), а второе - амплитуду автоколебаний в зависимости от коэффициента уснле1И-1я к и от других параметров системы.

Заметим, что во всех случаях, рассмотренных в примере 5 и в данном примере релейной систе.мы, через а обозначачась а.мплитуда автоколебаний вешчиных. А.мплитуда же автоколебаний Яд управляемой величирпл 9 (температуры) будет

Ux<u2<u3

П р И .м е р 7. Рассмотрим систе.му автоматического управления с приводом регу-JHipyraujero органа в виде двухфазного двигатечя перемстпюго тока. Характеристика этого двигателя для разных значений уг1равля1оП1его напряжения и имеет вид, представленный иа рис. 18.23, а.

Линеаризуя характеристики, обычно считают

M = c,f/-c.2a), . (18.116)

Но это справед;1ИВо в первом приближении только для левого участка характеристики. Если же используется большая часть характеристики, то необходимо учесть ее нелинейность. Имея в виду, что на рис. 18.23, а с увеличением (Одв коэффициент с, уменьшается, а коэффициент увеличивается, примем для описания .этой характеристики вместо (18.116) следующее нелинейное выражение:

М = -

1-1-Сз

[/-(с2+С4а)дз)а) (18.117)

(абсолютные значения Юд в коэффициентах поставлены потому, что (Од меняет знак, а сами коэф(})ициепты должны оставаться положительными). Аналогично можно под-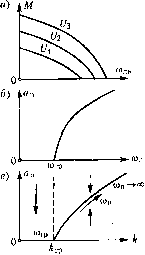