й, с

Итак, установившийся режим стабилизации в данной системе является автоколе-бательньш. Однако уравнениесистемы (17.13) справедливо только для идеальной системы стабилизации. Всякое реально имеющееся .запаздывание в работе усилительно-преобразовательного и исполнительного устройств приведет к увеличению амплитуд автоколебаний по сравнению с полученными .здесь значениями. Решение задачи с учето.м постоянных времени системы управления будет дано в следуюптей главе.

Пример 3. Уравнения системы автоматического управления курсом торпеды в упрошенном варианте имеют вид: линейная часть (16.40) и (16.41), т. е.

Тр\ + = -ib,5, .v = 2¥. (17.20)

и нелинейное звено (возьмем сначала один случай - рис. 16.18, в)

8 = csign(s-i) при ps>0,

(1721)

5 = csign{s + h) при ps<0.

Далыле {4-5) процесс пойдет с постоянной скоростью (так как Ф 0), после чего тело войдет в установив1пнйся автоколебательный режим, определяемый предельным циклом (5-б-7-($). Уравнение параболы 7-(Sсогласно (17.15) будет

Отсюда амплитуда угловых автоколебаний а, как значепие ф при (0 = 0, будет

Ф=й + , (17.19)

а амплитуда колебаний скорости = й,.

Она равна зоне нечувствительности датчика угловой скорости й в то время как амплитуда угловых колебаний (17.19) несколько больше зоны нечувствительности измерителя угла й.

Период автоколебаний t можно вычислить как сумму вре.мен:

где гол И ~ времена участков {6-7) + {8-5) и {5-6) + {7-8) соответствеппо.

11о законам равномерного и равнозамедленного движигий соответствеппо гюлучае.м

й 8 УРЧ

EiE S

в) у=ру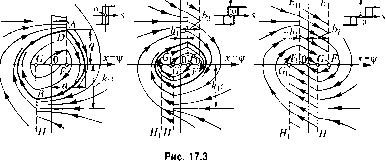

Покажем, что .здесь равновесное установившееся состояние системы с постояины.м значением \\i = 0 неустойчиво, по будет иметь место автоколебательный процессе,

Во.зьме.м фазовую плоскость (х.у) с коордипата.ми .г = \, у =рЦ1 (угол отклонения и угловая скорость отклоне1П1я оси торпеды отзадатюго курса). Уравнения (17.20) и (17.21) перепишутся в виде

dt dt 7; г,

5 = с sign

5 = с sign

h х + -

при у>0,

ири у>0.

(17,22)

Из сравнения этих уравнений с упрошенными уравнениями систе.мы стабилизации температуры в конце § 16,1 видна их полная аначогия. Поэтому здесь, так же как и в случае рис, 16.15, установившийся процесс движения торпеды будет автоколеба-тел1>иым, причем картина фазовых траекторий будет иметь вид, показанный па рис. 17.3, а.

При этом кривая Л/i предельного цикла, соответствующая автоколебательному процессу, определяется из уравнения (16.31) с таким значением прои.звольной постоянной С чтобы выполнялось условие

Уа = -Ун 1 . е. (у)

h =-{у)

(17.23)

так как только в это.м случае и получится .замкнутая кривая предельного цикча ABD (рис. 17.3, а). Определив чаким образом 6 найдем амплитуду автоколебаний а как значениеX при г/ = О, т. е. согласно (16.31)

а = ксТ In kc + Cj.

что соответствует нак.тониым 11рям1,1м внутри полосы EFFE па фазовой плоскости (рис. 17.3, б). Аналогичная полоса HGGH будет и в нижней части плоскости. Все оста;п>пое запо;н1яется таки.ми же кривыми, как па рнс. 17.3, а. В результате с увеличением зоны нечувствительности размеры предельного цикла, а значит, и амплитуда автоколебаний уменьшаются. При />, = О предельный цикл вырождается в точку О.

При да.тьнейп1е.м увеличении зоны нечувствительности характеристика пелиней-П010 звена и картина фазовых траекторий принимают вид, показанный па рис. 17.3, в. Здесь автоколебания отсутствуют и ста1К)вится устойчивым установивптйся процесс с постоянны.м значением V/. Ранее неустойчивый особый отрезок f, Gтеперь стал устойчивым. Дальнейшее увеличение зоны нечувствительности приводит к расширению отрезка Е G, т. е. к увеличешно установив1нейся оип1бки систе.мы из-за слишко.м широкого участка равновесия.

При .м е р 4. Рассмотрим систему стабилизации напряжения, уравнения которой были составлены ц§ 16.2, а и.мешю:

(7;/л-1)А(/=-А,Аг,

(17.24)

риче.м уравнение нелинейного звена (унра1!..тяющего органа)

A7- = ;j sign(A72-г,) при >0,

Аг = г, sign(A/2 -I- ь) при < 0.

(17.25)

В качестве ординаты фазовой плоскости здесь удобнее взять пе скорость отклоне-

л/ ы

ния управляемой величины как делалось [)аньше, а вторую переме1нгую Д/2- итак, примем д;1Я этой .задачи

х = М1, y = Ah О-б)

Тогда уравнения (17.24) преобразуются к виду

dx 1 , , . , - = --(.r-t-A,Ar),

dt 7

(17.27)

Значения же (17.23) дают а.милитуду q колебат-гй скорости у. Можно все то определять и графически прямо по чертежу (рис. 17.3, а). Период автоколебаний остается пеи.звестиы.м.

Введем теперь в характерист1П<у нелииейио1-о звена (рулевой мацн1ики) зону нечувствительности, как показано па рнс. 17.3, б, в. 1 ак, па то.м участке характеристики 5 =/(5) (рис. 17.3, б), где 5 = 0, из (17.22) следует, что