Ко1)1[И характеристического уравнения, расположенные ближе всего к aиIoй оси, т. е. имеюнню наименьшую по абсолютной величине вепюствепную часть, дают в переходном процессе (7.3) члены, которые затухают наиболее медленно. В болышшстве случаев переходный процесс .можно считать .закончившимся тогда, когда .затухнет член, определяемы!! ближайшим к мни.мой оси корпе.м. Если ближайшим к мни.мой оси является вешественный корень, то составляющая в переходпо.м процессе, определяемая этим корнем, будет и.меть видх(0 = Су.

Положив в конце переходного процесса х(? ) = АС где А = 0,01 0,05, можно получить приближенную зависимость между степенью устойчивости и временем переходного процесса:

11 1

t =-1п-.

(8.30)

Так, нанри.мер, если принять Д = 0,05, то время переходного процесса составит

1, 13

--1п-Л 0,05

Если ближайшей к мнимой оси является па[)а комплексных корней -г\ ±уР, то составляющая в переходном процессе, определяемая этими корня.ми, будет xiO = Ce-siH(pr +V).

Положив в этом случае Xr,(f) = АС, нельзя в обп1е.м виде определить В1)емя nei)C-ходного процесса, так как для этой цели потребовалось бы решить трансцендентное уравпение. Однако може.м найти верхнюю rpaininy переходного процесса, положив в .этом уравненин sin(P -ь у) = 1. Тогда получим выражение

(8.31)

Таким образом, и в этом случае величина степени устойчивости будет в какой-то .мере оп])еделять быстроту затухания пе[)еходного процесса.

Более строго связь между видом переходного процесса и величиной степени устойчивости .может быть оиределепа для случая, когда исходное диф(})еренциалы1ое уравнение системы и.меет вид

.1-1

)л(0 /(0,

(8.32)

Тогда можно показать [44], что при всех вепюственных корнях или одной паре комплексных корней для переходной функции справедливо неравенство

1 + v(Ti, t) > /КО > 1 - v(n. 0. (8.33)

где 1 + v(ri, О - функция, ограничивающая h{t) сверху (мажоранта); 1 - v(ri, О - функция, ограничивающая h{t) спи.зу (.миноранта).

Вспомогательная функция v(r\, t) определяется из выражения v(Ti,0 = e

{r\t.f (TiO

( -l)!

(8.34)

Миноранта совпадает с переходной функпией, если характеристическое уравнение имеет корень р,= -У] кратности п, т. е. выглядит следующим образом:

anlf + аУ Ч ... + а = ао(р + Ц) = 0. (8.35)

Очевидно, что в этом случае п-кртшИ корень совпадает со среднегеометрическим корпе.м

(8.3G)

Из неравенства (8.33) вытекает, что при заданном значении среднегеометрического корпя £2ц = const и всех вещественных корнях наи.мспьшее время переходного процесса будет ирп всех кратных корнях, т. е. в случае (8.35).

На рис. 8,7 приведены .миноранты, совпадающие с переходными характеристи-ка.ми для случая и-кратного корня, построенные в функции относительного времени т = Qt для различных значений порядка дифференциального уравнения п.

Важным обстоятельством является то, что степень устойчивости можно найти без вычисления значений корней характеристического уравнения. Для этой цели в характеристическом уравпепий (8.25) переходят к повой неремениой z=p + г\. Подставляя в него 2 = р - У], получаем так иазынаемое смиценное уращ1епие

о (2 л) + а,{2 - л) + ... + (2 - Л) + - 0.

Раскрывая скобки и группируя подобные члены, получаем

Это уравнение соответствует смещению осей на плоскости корней (рис. 8.6) влево па величину У]. В результате один (рис. 8.6, а) или два (рис. 8.6, б) корня попадают на мнимую ось, что соответствует границе устойчивости.

Для вычисления степени устойчивости необходимо при.меиить к смещенжзму характе-ристическо.му уравнению (8.37) любой критерий устойчивости и определить, при каком значении г\ получается граница устойчивости. Напомпи.м, что апериодической rpainme устойчивости соответствует равенство нулю свободного члена характеристического уравпепия: Л.

(8.37)

О, (8.38)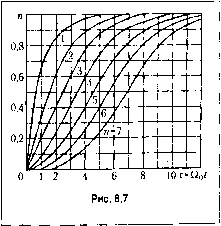

Через один период Т= 2я/Р

С 2 ~ Се

= С,е Р =С,е .

Затуханием за период называют величину

С, -С2 С2

C = V = l-7r- (8.40)

Эта величина обычно выражается в процентах. Подставляя значение амплитуды С2, получаем

-- (S.42)

Обычно в системах автоматического управления допускается затухание за один период не менее чем 90 98%. Так, например, если С% = 98%, то допустимая колебательность при этом составит

2л л ,

а колебательной rpainme устойчивости соответствует равенство пулю предпоследнего определителя Гурвица или прохождение амплитудно-фазовой характеристики разомкнутой системы через точку (-l,j0).

Обратимся теперь к оценке запаса устойчивости системы автоматического управления. Склонность систе.мы к колебаниям будет наблюдаться, если в решепии хараетеристического уравнения будут присутствовать комплексные корни вида -а ± jp. Эта склонность может характеризоваться отношением .мпи.мой части корня (угловой частоты колебаний) к венюственной (коэффициенту затухания), которое называется колебательностью:

р = Р/а. (8.39)

Колебательность связана с другим корпевы.м показателем запаса устойчивости - с так HasbiBaeMbi.vi затуханием. Комплексные сопряженные корни даюг в выражении для переходного процесса член вида

.г(0 = Се- sin(p/: + v).

Найдем затухание амплитуды синусоидального колебания за один период. При некотором вре.мени t = эта амплитуда равна