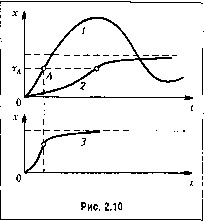; Нелинейные алгоритмы управления обладают богатыми возможностями во всех случаях, когда требуемый эффект может быть достигнут изменением свойств системы с изменением величин ошибок.

Большие дополнительные возможности улучшения процессов управления даетнелинейное управление работой объекта путем изменения структуры управляющего устройства в зависимости от размеров и знаков входных величин, поступающих от измерительного устройства.

При это.м могут использоваться комбинации линейных алгоритмов управления. Например, если известно, что при одном линейном алгоритме получается быстрое начальное из.менение управляемой величины, по с больши.ми последующими колебаниями (кривая 1, рис. 2.10), а при другом линейном алгоритме - медленное изменение, но плавньнг подход к пово.му установившемуся режиму (кривая 2, рис. 2.10), то можно, включив сначала первый алгоритм, переключить затем систему на второй алгоритм в некоторой точке А, когда отклонение х достигнет определенного значения х. В результате процесс изобразится кривой 3 (рис. 2.10), объединяющей оба качества - быстроту и плавность процесса. Для осуществления этого необходимо иметь в системе переключающее устройство, срабатывающее при х = (рис. 2.11).

Если в такой системе все звенья линейные, то за счет указанного переключения, происходящего автоматически в процессе управления, система становится нелинейной. Это можно сравнить с тем, как получается нелииейпая статическая характеристика из отрезков пря.мых линий. Но здесь и.меет место нелинейная динамическая характеристика, составляемая из последовательности разных линейных дифференциальных уравнений, соответствующих первому и второму алгоритмам управления.

В общем случае срабатывание переключающего устройства в системе с перемеп-Пой структурой может происходить от нескольких входных величин. При этом кроме основной нелинейности, возникающей за счет переключения структуры, дополнительно могут иметься какие-либо пелинейиые свойства в отдельных других звеньях управляющего устройства или объекта.

Исполн, устр.

Управляемый объект

РАЗДЕЛ

НЕПРЕРЫВНЫЕ ЛИНЕЙНЫЕ СИС

АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Глава 3

ЛИНЕАРИЗАЦИЯ

ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

§3.1. Линеаризация уравнений

При составлении диф(})ереициальных уравнений динамики ;иобой автоматической системы последнюю разбивают на отдельные звенья и записывают уравнение каждого звена в отдельности. Уравнения всех звеньев образуют единую систему, которую можно преобразовать к одпо.му уравнению путем исключения промежуточных переменных.

Уравнение звена должно быть составлено так, чтобы оно выражало зависимость (в динамическом процессе) между теми величинами, которые в схеме исследуемой системы указаны на выходе и входе данного звена, т. е. между величинами, представляющими воздействие данного звена на последующее по схеме звено и воздействие предыдущего звена па данное Дина.мическое уравнение отдельного звена составляется но правилам соответствующей технической пауки (звено может представлять собой тепловой двигатель, электрическую мапншу, механическую передачу, электрическую цепь и т. п.).

Звено .может и.меть иногда пе одну входную величину, а несколько (например, при наличии дополнительных обратных связей). Кроме входной н выходной величин звена, которые выражают собой впутрегщие связи между звеньями данной системы, может учитываться также внещнее во.здействие.

Пусть, напри.ме]), звено (рис. 3.1, а) какой-нибудь авто.матической системы имеет входные величины х Xg, выходную - и впентее воздействие/, а динамическое Уравнение звена имеет произвольный нелинейный вид

f (Xi, Х2, Х2, 3, ±3, 3 Хз) = ф(/, /)

(3.1)

(для примера взятонределеипый порядок входящих в уравнение производныхХ2,Хз, /; вообще же здесь .могут быть любые д])угие варианты).

Допустим, что установившийся процесс в системе имеет место при некоторых постоянных значениях .г, =х},

.го = x

огда уравне-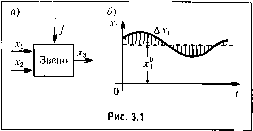

ние установившегося состояния для данного звена согласно (3.1) будет

f(x°,xi,0,X2°,0,0,0) = 9(/°,0). (3.2)

В основе линеаризации нелинейных уравнений лежит предположение о то.м, что в исследуемом динамическом процессе переменные (в данном случае х Х2, Х3) изменяются так, что их отклонения от установившихся значений (xf,.r2,xjj остаются все

время достаточно малыми (рис. 3.1, б).

Обозначим указанные отклонения через Дх Axj, Дх. Тогда в динамическом процессе

Х,(0 = Х+ЛХ,(0, Х2(С) = Х+ДГ2(0, Х2=АГ2,

хз(0 = 4 + 3(О. = А-гз, хз = Дхз, хз = Ai-з.

(3.3)

Условие достаточной .малости дина.мических отклонений переменных от некоторых установившихся значений для систе.мы автоматического управления обычно выполняется. Этого требует са.ма идея работы замкнутой автоматической системы.

Bneuniee же воздействие/ не зависит от работы автоматической системы, изменение его .может быть произвольным, и поэтому правая часть уравнения (3.1) обычно линеаризации не подлежит (в отдечьных случаях и она может быть линеаризована).

Первый способ линеаризации. Разложим функцию F, стоящую в левой части уравнения (3.1), в ряд по степе1шм указа1Н1ых выше малых отклонений, рассматривая все производные тоже как са.\юстоятелып>1е переменные. Тогда, уравнение (3.1) примет вид

/(xf, Х2°,0, хз°,0. О, О)-

Дх, +

jx-

АХ2 +

л-

Ar.j -ь

ах.,

Ахз -<-

Дхз -ь

уЭХзу

Дх., -t-

+ члены высше1-о порядка .малости) = ф(У./),

(3.4)

{ЪFЛ

хЪху

dF о

для краткости обозначена величина --, взятая при х, = .г,

где через

Х2=Х2, Х2=0, Хз = х ,..., Хз =0 (т. С. спервз берется в общем вид частная произ-